Eigenvalues and Eigenvectors
Definitions
If L is a linear transformation from a vector space to itself, then of interest is whether there are any vectors v have the property that L(v) is a multiple of v. If this is the case then repeatedly applying L will result in a vector always parallel to v. This idea is if fundamental importance for applications in physics, mechanics, economics, biology, and just about every other scientific field. We can state this in terms of matrices as follows.
Let A be an n x n matrix. Then a scalar l is called an eigenvalue with associated nonzero eigenvector v if
Av = lv
Example
For the matrix
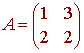
we can check that -1 and 4 are eigenvalues with associated eigenvectors
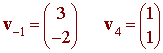
Notice that if v is an eigenvector with eigenvalue l, then so is any multiple of v since
A(cv) = cAv = c(lv) = l(cv)
Example
The identity matrix In has 1 as its only eigenvalue. All vectors are associated eigenvectors since
Inv = v = (1)v
for all v.
Finding Eigenvalues and Eigenvectors
We will now determine how to find the eigenvalues and eigenvectors for a matrix. Let A be a matrix with eigenvalue l and eigenvector v. Then
Av = lv
implies that
Av - lv = 0
We would like to factor out a v from the above (right) equation. However, we must be careful because the term A - l does not make sense. Instead we have
(A - lI)v = 0
If there is a nontrivial solution, then
det(A - lI) = 0
and the solution is in the null space of A = lI.
Example
Find the eigenvalues and eigenvectors of
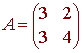
We have
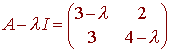
which has determinant
(3 - l)(4 - l) - 6 = l2 - 7l + 12 - 6
= l2 - 7l + 6 = (l - 1)(l - 6)
So the roots are
l = 1 and l = 6
Now lets find the eigenvectors. For l = 1, we have
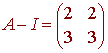
which has rref
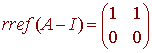
A nonzero vector in the null space is
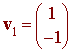
Now for the eigenvector corresponding to l = 6. We have
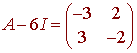
Notice that the second row is redundant. At this point it is pretty easy to see that
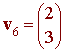
notice that there are lots of choices for these vectors (all multiples the above vector). We made our choice in order to avoid fractions.
The Characteristic Polynomial
We have seen that in order to find the eigenvalues, we just find the roots of the polynomial defined by
pA(l) = det(lI - A)
We call this polynomial the characteristic polynomial. The degree of the polynomial will be n where A is an n x n matrix. The roots of the characteristic polynomial will be the eigenvalues. Notice that if 0 is a root then
det(0I - A) = det(A) = 0
This tells us that 0 is an eigenvalue if and only if det(A) = 0. We can now add one more statement to the nonsingular equivalents.
Let A be an n x n matrix. Then TFAE
- A
is nonsingular.
- Ax
= 0 has only the
trivial solution.
- A
is row equivalent to I.
- Ax
= b has a unique solution
for all b.
- det(A)
is nonzero.
- A
has rank n.
- A
has nullity 0.
- The
rows of A
are linearly independent.
- The
columns of A
are linearly independent.
- 0 is not an eigenvalue of A.
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions