Diagonalization

Similar Matrices

We have seen that the commutative property does not hold for matrices, so that if A is an n x n matrix, then 

        P^-1AP

is not necessarily equal to A.  For different nonsingular matrices P, the above expression will represent different matrices.  However, all such matrices share some important properties as we shall soon see.

Definition

Let A and B be an n x n matrices, then A is similar to B if there is a nonsingular matrix P with

        B  =  P^-1AP

Example

Consider the matrices

Then 

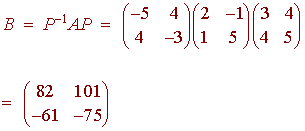
is similar to A.

Notice the three following facts

1. A is similar to A.
   
   
2. If A is similar to B then B is similar to A.
   
   
3. If A is similar to B and B is similar to C then A is similar to C.

We call a relationship with these three properties an equivalence relationship.  We will prove the third property.

If A is similar to B and B is similar to C then there are matrices P and Q with

        B  =  P^-1AP        and        C  =  Q^-1BQ

We need to find a matrix R with 

        C  =  R^-1AR

We have

        C  =  Q^-1BQ  =  Q^-1(P^-1AP)Q  =  

        (Q^-1P^-1)A(PQ)  =  (PQ)^-1A(PQ)  =  R^-1AR

There is a wonderful fact that we state below.

Theorem

If A and B are similar matrices, then they have the same eigenvalues.

Proof

It is enough to show that they have the same characteristic polynomials.  We have

        det(lI - B)  =  det(lI - P^-1AP)  =  det(P^-1lIP - P^-1AP)

        =  det(P^-1(lI - A)P)  =  det(lI - A)

Diagonalized Matrices

The easist kind of matrices to deal with are diagonal matrices.  Determinants are simple, the eigenvalues are just the diagonal entries and the eigenvectors are just elements of the standard basis.  Even the inverse is a piece of cake (if the matrix is nonsingular).  Although most matrices are not diagonal, many are diagonalizable, that is they are similar to a diagonal matrix. 

Definition

A matrix A is diagonalizable if A is similar to a diagonal matrix D.

        D  =  P^-1AP

 The following theorem tells us when a matrix is diagonalizable and if it is how to find its similar diagonal matrix D.

Theorem

Let A be an n x n matrix.  Then A is diagonalizable if and only if A has n linearly independent eigenvectors.  If so, then 

        D  =  P^-1AP

If {v₁, ... , v_n} are the eigenvectors of A and {l₁, ... , l_n} are the corresponding eigenvalues, then 

        v_j the j^th column of P 

and 

        [D]_jj  =  l_j 

Example

In the last discussion, we saw that the matrix

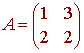
has -1 and 4 as eigenvalues with associated eigenvectors

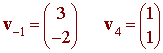
Hence

        D  =  P^-1AP

Proof of the Theorem

If 

        D  =  P^-1AP

for some diagonal matrix D and nonsingular matrix P, then

        AP  =  PD

Let v_i be the j^th column of P and [D]_jj  =  lj.  Then the j^th column of AP is Av_i and the j^th column of PD is l_iv_j.  Hence

        Av_j  =  l_iv_j 

so that v_j is an eigenvector of A with corresponding eigenvalue l_j.  Since P has its columns as eigenvectors, and P is nonsingular, rank(P)  =  n, and the columns of P (the eigenvalues of A) are linearly independent.

Next suppose that the eigenvalues of A are linearly independent.  Then form D and P as above.  Then since 

        Av_j  =  l_iv_j 

The  j^th column of AP equals the j^th column of PD, hence AP  =  PD.  Since the columns of P are linearly independent, P is nonsingular so that

        D  =  P^-1AP

Theorem

Let A be an n x n matrix with n real and distinct eigenvalues.  Then A is diagonalizable.

Proof

Let 

        {l₁, ... , l_k}   and    {v₁, ... , v_k}

with

         rank(Span({v₁, ... , v_k}))  =  k - 1

be the eigenvalues and eigenvectors of A.  We need to show that none of the vectors can be written as a linear combination of the rest.  Without loss of generality, we need show that the first can not be written as a linear combination of the rest.  If

         v₁ = c₂v₂ + ... + c_nv_k         (1)

We can multiply both sides of the equation by A to get 

         l₁v₁ = Ac₂v₂ + ... + Ac_nv_k  =  c₂l₂v₂ + ... + c_nl_nv_k         (2)

Multiply (1) by l₁ and subtract it from (2) to get

        c₂(l₂ - l₁)v₂ + ... + c_n(l_n - l₁)v_n = 0

Since the l's are distinct, the c_i's must all be zero, which is a contradiction (otherwise the rank would be less than k - 1).  Hence 

         rankSpan({v₁, ... , v_k})  =  k

for any k.  In particular, let k  =  n, and the result follows.

Note that the converse certainly does not hold.  For example, the identity matrix I has 1 as all of its eigenvalues, but it is diagonalizable (it is diagonal).

Steps to Diagonalize a Matrix

1. Find the eigenvalues by finding the roots of the characteristic polynomial.
   
   
2. Find the eigenvectors by finding the null space of A - l_iI.
   
   
3. If the number of linearly independent vectors is n, then let P be the matrix whose columns are eigenvectors and let D be the diagonal matrix with [D]_jj  =  l_j
   
   

Example

Diagonalize the matrix

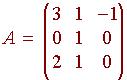
Solution

We find the characteristic polynomial

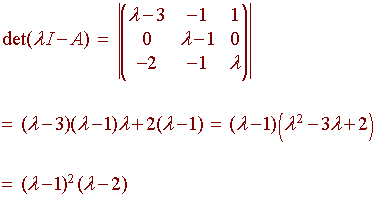
The roots are 1 (with multiplicity 2) and 2 (with multiplicity 1).

Now we find the eigenspaces associated with the eigenvalues.  We have

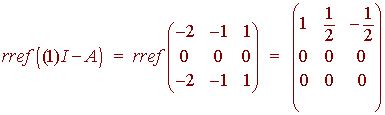
A basis for the null space is 

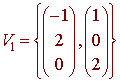
Next we find a basis for the eigenspace associated with the eigenvalue 2.  We have

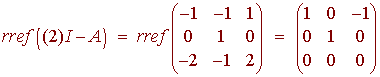
A basis for this null space is

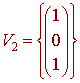
Now put this all together to get

Back to the Vectors Home Page

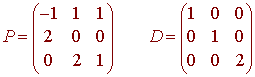
Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions