Conic Sections

The Problem

We all know how to sketch the graph of an ellipse or hyperbola given an equation such as 

        x² + 2y² + 4x + 12y + 6  =  0

by completing the square, finding the center of the ellipse, plotting the vertices and sketching the graph.  If you forgot this process click here.  The goal of this discussion is to be able to sketch a conic section given by 

        ax² + 2bxy + cy² + dx + ey + f  =  0

The fact that there is an xy term here poses the challenge.  We will look at the example 

Our goal is to graph this conic.  At this point, we do not even know if it is a hyperbola, ellipse, or circle.  The type will come out soon enough.

The Solution

The key to solving this is to realize this as a matrix equation:

        x^TAx + Bx + f  =  0

Where A is a 2 x 2 matrix, B is a 1 x 2 matrix and x^T  =  (x,y).  For our example we have

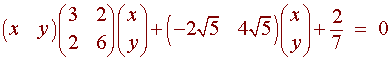
Next we diagonalize the matrix A.  Since the matrix is symmetric, it can be orthogonally diagonalized.  The eigenvalues are 7 and 2.  We can check that the diagonalization is given by

        A  =  PDP^T

or

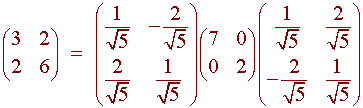
We can write

        x^TAx  =  x^TPDP^Tx  =  (P^Tx)^TD(P^Tx)

and let

        y  =  P^Tx        or        x  =  Py

That is

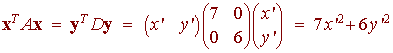
and

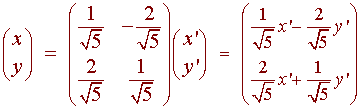
So that 

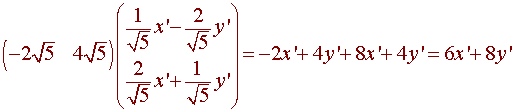
We can put this all together to get

        7x'² + 2y'² + 6x' +8y' - 2/7  =  0

Completing the square gives 

        7(x' + 3/7)² + 2(y' + 2)²  =  9

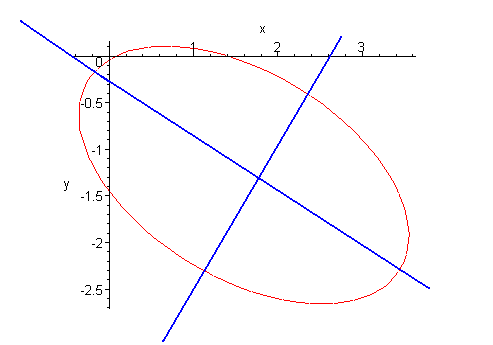
This is the ellipse centered at (-3/7, -2) in the (x', y') coordinate system.  with 

        a  =  3 /        b  =  3 /

The effect of the change of coordinates is a rotation of the graph by an angle of 

        arctan(-2)  =  -1.1

The value of -2 was obtained by finding P₂₁/P₁₁.  The graph is shown below.

Eigenvalues and Types of Conics

In algebra, we learn how to identify conics.  If the signs are opposite then we get a hyperbola and if the signs are alike, but the coefficients are different, we get an ellipse.  If the signs are the same, we get a circle.  If there is an absence of a squared term, then we have a parabola.  We have a similar classification system for our rotated conics.

Theorem

Let 

        x^TAx + Bx + f  =  0

be a conic and let 

        s  =  l₁ l₂ 

then 

• If A is the zero matrix, we have a line.  Otherwise
  
  
• If s < 0 the conic is a hyperbola
  
  
• If s > 0 then we get an ellipse (possibly degenerate) that is a circle if the eigenvalues are equal.
  
  
• If s  =  0 then we get a parabola

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions