Graph Theory
We now delve into our first application or matrices, graph theory, which shows its face in communications, sociology, business, transportation sciences, and many other fields. We begin by stating the basic definitions.
A directed graph, also called a digraph, is a set of points P1, P2, ... , Pn called vertices and ordered pairs of points PiPj called edges.
A digraph can have a vertex that does not belong to any edge or two points that are connected by edges in both directions.
Example
The digraph with points P, Q, R, S, and edges PQ, QP, PR, and QR is shown below.
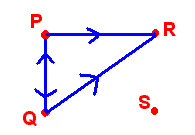
Let G by a digraph with n vertices, then the adjacency matrix of A, written A(G), is the n x n matrix with A(G)ij equal to 1 if PiPj is an edge and zero otherwise.
Example
The adjacency matrix of the graph in the example above is
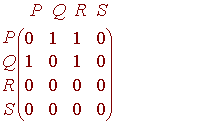
Example
Five students, Aurellio, Brian, Cindy, Dave, and Edward have formed a study group. Aurellio has Cindy and Dave's phone number, Brian has Edward's number, Cindy has Dave and Edward's number, Dave has Aurellio and Brian's number and Edward has everyone's number.
The graph and the adjacency matrix are shown below.
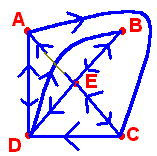
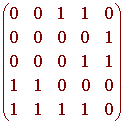
One of the questions that we may ask, is if Aurellio wants to get a hold of Brian, how can he do this? More specifically we can ask how many ways are there of Aurillio getting Brian's number using no more than two edges.
We say that Pi has r stage access to Pj if there is a way to get to Pj from Pi via r edges.
The following theorem helps us to answer the question at hand.
Theorem
Let A(G) be the adjacency matrix of a digraph G then the number of r stage accesses that Pi has to Pj is given by
[A(G)r]ij
Thus the total number of ways that Pi has access to Pj in r or fewer stages is the ijth element of the matrix
A(G) + A(G)2 + ... + A(G)r
Now back to our problem. We have
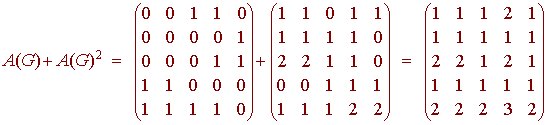
To find out how many ways there are of Aurillio getting Brian's number using no more than two edges we just take the 1 2th element of this matrix. This is 1, so there is exactly one way of Aurillio getting Brian's number using no more than two edges.
Sociologists speak of cliques, which mean subgroups of a larger group that associate with each other but do not associate with others. In the language of graph theory we have the following.
Definition
A clique in a digraph is a subset S of the vertices satisfying the following three properties
- S
contains three or more vertices.
- If Pi
and Pj
are in S then
Pi
has access to Pj then
Pj
has access to Pi.
- There is no larger subset containing S that satisfies properties 1 and 2.
Example
In the digraph below, B, C, D, and E form a clique.
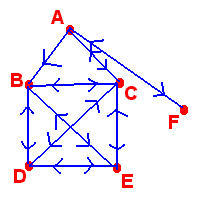
In the above example, it is relatively easy to spot any cliques. For larger digraphs, it is much more difficult to spot a clique just by looking. Fortunately, there is a way of doing this using matrices.
Theorem
Let A(G) be the adjacency matrix of a digraph and let S by the matrix whose entries are defined by
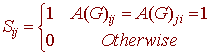
Then a vertex Pi belongs to a clique if and only if sii3 is nonzero.
Example
Consider the diagraph with adjacency matrix
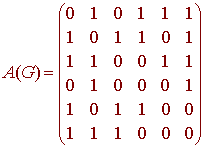
Then
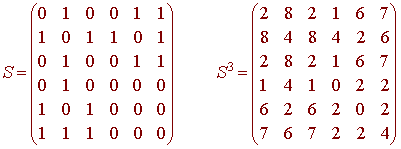
We see that the positive diagonal elements correspond to P1, P2, P3, and P6. So these four vertices are in a clique.
Strongly Connected Graphs
If G is a graph then we are often concerned with ensuring that there is a path from any vertex to any other vertex. If the vertices represent street corners and the edges represent roads, then a civil engineer wants to ensure that a car can get from any street corner to any other corner. This idea also applies to networked systems such as telephone lines.
A graph is called strongly connected if for every two distinct vertices Pi and Pj there is a path leading from Pi to Pj and from Pj to Pi. Otherwise they are not strongly connected.
If there is a path that leads from Pi to Pj then at some stage Pi has access to Pj so that A(G)r will be positive. Moreover, since there are n vertices, the shortest path will contain fewer than n edges. This leads us to the following theorem.
Theorem
Let G be a digraph and A(G) be its adjacency matrix, then G is strongly connected if and only if
A(G) + A(G)2 + ... + A(G)n-1
has no zero entries.
Example
Consider the digraph below
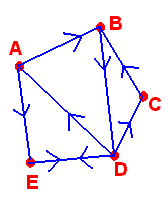
The adjacency matrix is
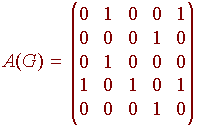
Now use a calculator to find
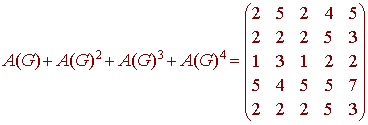
We see that this matrix has no zero entries, so the graph is strongly connected.
Back to the Matrices and Applications Home Page
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions