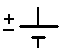
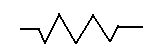
Electrical Circuits
This discussion will focus on using matrices to answer questions related to electrical circuits. We will provide the basic ideas from physics and see how matrices are useful in this subject. An electrical circuit consists of several components some of which are
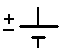
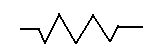
A battery provides current (in volts) to the circuit, a resister converts electrical energy into other useful energy such as light reducing the current, and a wire allows the current to flow through it without increasing or reducing the current. The example below shows an electrical circuit diagram.
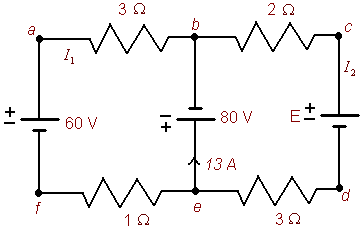
In this circuit diagram there are three batteries and four resisters. As you will notice the diagram contains plenty of additional notes. The batteries' electrical potential difference is measured in volts. The battery to the left is a 60 volt battery, the middle battery is an 80 volt battery, and the voltage of the battery to the right has yet to be determined. The resisters are measured in ohms. We use the Greek letter W as the unit indicator. The currents I1 and I2 are measured in amperes. In the diagram above the both currents have yet to be determined.
You will also notice the letters a, b, c, d, e, and f labeled on the circuit diagram. These mark important points in the diagram. Points b and e represent nodes. A node is a point where three or more wires connect. Points a, c, d, and f are not nodes, however as we shall see next, it is convenient to label them.
A voltage loop is a closed connection within a circuit. That is a piece of the circuit beginning at a point and ending at the same point. We will be interested in loops that do not contain any sub loops. There are two such loops in the above diagram:
a ---> b ---> e ---> f ---> a
and
b ---> c ---> d ---> e ---> b
A change in voltage occurs when a current passes through a battery. For example, on the 60 volt battery, a current flowing upwards (from "-" to "+") will gain 60 volts while a current flowing downwards (from "+" to "-") will lose 60 volts.
The voltage through a resistor is related by
V =
![]() IR
IR
The sign is positive if the measurement is taken against the current flow and the sign is negative of the measurement is taken in the direction of the current flow.
Kirchhoff came up with two law for electrical circuits that will help us find the unknown quantities.
Kirchhoff's Voltage Law: Around any voltage loop, the total electrical potential difference is zero.
Kirchhoff's Current Law: At any current node, the flow of all currents into the node equals the flow of all currents out of the node.
The first law is often called conservation of energy and the second law is often called conservation of charge.
We now have all the ingredients necessary to solve our problem. We will use Kirchhoff's two laws and the help of matrices to find the unknown currents and voltage. First we give a direction to the two currents. Later we may change the directions. Let I1 flow from e to f to a to b and let I2 flow from b to c to d to e. We begin with the loops. Consider the loop
a ---> b ---> e ---> f ---> a
From a to b, the current I1 passes through a resistor of 3 amps hence the potential difference is
-3I1
From b to e, the current passes though a battery with an 80 V voltage drop will have a potential difference of
80
From e to f the current passes through a resistor of 1 amp hence the potential difference is
-I1
From f to a, the current passes though a battery with an 60 V voltage gain will have a potential difference of
60
Kirchhoff's voltage law tells us that
-3I1 + 80 - I1 + 60 = 0
or
-4I1 = -140
Using Kirchhoff's voltage law on the loop
b ---> c ---> d ---> e ---> b
-2I2 - E - 3I2 - 80 = 0
or
5I2 + E = -80
Now we use Kirchhoff's current law. For the node b, the sum of the currents going in are
I1 + 13
and the current going out is
I2
So that
I1 + 13 = I2
or
I1 - I2 = -13
The node e gives
I2 = I1 + 13
Notice that this gives us no new information. We have the three equations
-4I1
= -140
5I2
+ E = -80
I1
- I2 = -13
This can be written in matrix form as
![matrix [(-4,0,0),(0,5,1),(1,-1,0)]matrix[(I_1),(I_2),(E)]=matrix[(-140),(-80),(-13)]](imgA.gif)
or with the augmented matrix
![Matrix[(-4,0,0|-140),(0,5,1|-80),(1,-1,0|-13)]](imgC.gif)
Now we can rref the matrix to get
![Matrix[(1,0,0|-35),(0,1,0,-22),(0,0,1|30)]](imgE.gif)
We have that
I1 = -35 I2 = -22 E = 30
Typically we want to present currents to be positive, so we change the orientation if I1 to go from b to a to f to e and say that I1 = 35.
Back to the Matrices and Applications Home Page
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions