Cofactors
Cofactors and Determinants
We begin with a definition.
Definition
Let A be an n x n matrix and let Mij be the (n - 1) x (n - 1) matrix obtained by deleting the ith row and jth column. Then det Mij is called the minor of aij. The cofactor Aij of aij is defined by
Aij = (-1)i+j det Mij
Example
Let
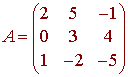
then
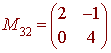
so the minor of a32 is the determinant of this 2 x 2 matrix. Since the matrix is triangular, the determinant is the product of the diagonals or
(2)(4) = 8
The cofactor is
A23 = (-1)2+3(8) = -8
One of the main applications of cofactors is finding the determinant. The following theorem, which we will not prove, shows us how to use cofactors to find a determinant.
Theorem
Let A be an n x n matrix and 1 < i < n. Then
det A = Sj (aijAij) = ai1Ai1 + ai2Ai2 + ... + ainAin
This theorem has little meaning without an example.
Example
Use cofactors to find det A for
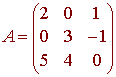
Solution
We can use any row that we want. Let's pick the second row. We have
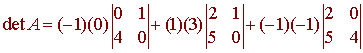
= 0 + (3)(0 - 5) + (8 - 0) = -7
Remark: Since det A = det AT, we can expand about a column if we desire.
Example
Find the determinant of
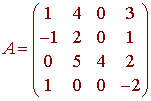
Solution
We can choose any row or column to expand. The third column has only one nonzero entry, so we select this column. We have
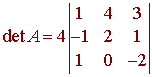
Now lets expand about the third row. We get
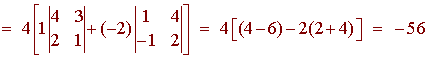
Cofactors and Inverses
Just as cofactors can be used to find the determinant of a matrix, they can be used to find the inverse of a matrix. We begin with a theorem that will be useful for proving the inverse formula.
Theorem
Let A be an n x n matrix. Then
ai1Ak1 + ai2Ak2 + ... +
ainAkn = 0 for i
![]() k
k
a1jA1k + a2jA2k + ... +
anjAnk = 0 for j
![]() k
k
Proof
We will prove the first statement for i = 1 and k = 2. The general case and the second statement can be proven in a similar way. We want to show that
a11A21 + a12A22 + ... + a1nA2n = 0
Consider the matrix B that is the same as A except that the second row of B is the same as the first row. Since two rows of B are repeated, the determinant of B is zero. Now find det B by expanding about the second row. You will notice that this expansion is
0 = b21B21 + b22B22 + ... + b2nB2n = a11A21 + a12A22 + ... + a1nA2n
and the theorem is proven.
Let A be an n x n matrix. Then the adjoint of A (adj A) is the matrix such that
(adj A)ij = Aji
Notice the switch of subscripts. This means that the adjoint is the transpose of the matrix that consists of cofactors.
Example
Find adj A for
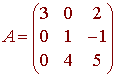
Solution
We have
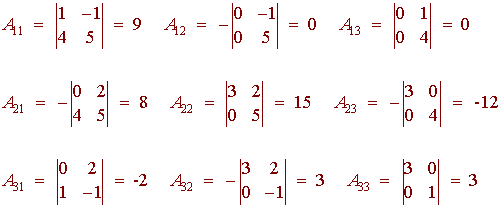
So that
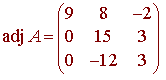
Now for the main theorem
Theorem
If A is an n x n matrix then
A(adj A) = (adj A)A = (det A) In
The proof follows immediately from the formula for the determinant and the previous theorem. We have
[A(adj A)]ij = Sk aik(adj A)kj = Sk aikAjk = (det A)dij
where dij is the Kronecker delta function evaluating to 1 for i = j and 0 otherwise. Hence the theorem is proven.
The main application of this theorem is the following corollary that easily follows from the theorem.
Corollary
If A is a nonsingular matrix then
1
A-1 =
adj A
det A
Example
We found that the matrix
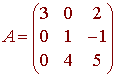
has adjoint
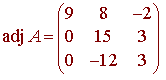
We can find that
det A = [A(adj A)]11 = 27
Hence
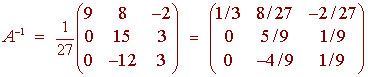
This gives us a way to find inverses and a way to determine if a matrix is nonsingular.
For a 2 x 2 matrix the adjoint of A is easy to find. We have
Using
the inverse formula, we get Theorem A
matrix is nonsingular if and only if the determinant is nonzero. Proof If
A is nonsingular, then
1 = det(I) = det(AA-1) = (det A)
(det A-1) so
the determinant of A is nonzero. If
the determinant is nonzero, then the corollary shows us how to find the inverse
so the matrix is nonsingular. This
gives us an addition to our list of nonsingular equivalences. Theorem TFAE We end this discussion with the statement of Cramer's Rule, a formula that
gives us the solution of systems of equations. Cramer's Rule Let Ax
= b be
a linear system of equations with n
x n matrix A.
Then the solution is
det(Ai) where
Ai is the matrix obtained from
A by replacing the
ith column of A
by b. Example
x - 3y + 2z = 3 Solution We
write this in matrix form
We
have
det A = 1(1 - 1) - (-3)(2 - 1) + 2(2 - 1) = 5 since
we want to find z, we need det
A3.
We
find z by dividing
20
Back
to the Matrices and Applications Home Page
Back
to the Linear Algebra Home Page
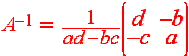
xi
=
det(A)
Use Cramer's rule to find z if
2x + y + z = 1
x + y + z = 3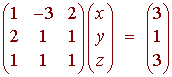
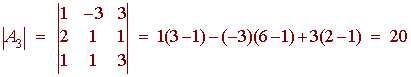
z =
= 4
5