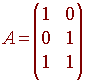
Code Theory
Code theory has become increasingly important as computers have become ingrained in our lives. This discussion will focus on error detection and correction rather than on encryption. When a message is sent over the net, it is encoded as a binary string of numbers. It is likely that a few of these numbers will become corrupted (a 1 becoming a 0 or a 0 becoming a 1). We will be looking at ways of detecting such an error and if possible correcting it. First a few definitions.
A message is a sequence of numbers where each of the numbers is either 0 or 1. We can encode a word by changing each of its letters as binary string. A sentence is a sequence of words, so any set of words can be represented by a vector. Typically we will send a message from one computer to another, however, because of noise, the message received will not always be the same as the message sent. In order to deal with this issue, we send a transmission that includes redundant bits so that we can detect when something has gone awry. The transmission will be a m by n matrix with m > n.
Example
Let A be the transmission matrix
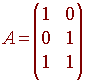
We have the following table:
| Message | Transmission |
| (0,0) | (0,0,0) |
| (1,0) | (1,0,1) |
| (0,1) | (0,1,1) |
| (1,1) | (1,1,0) |
If an entry in the transmission differs from what the entry was supposed to be transmitted, then we call this an error. Notice that if the receiver receives a transmission other than the four possible transmissions, then an error is detected. For example a transmission of (1,1,1) is detected as an error. The receiver will detect an error whenever there is exactly one error in the transmission. However if there are two errors, the error will not be detected. This is called a single error correcting code. Notice that the third component of the transmission is 0 if the sum of the entries of the message is even and 1 if the sum is odd. The sum of the entries is called the weight of the message. The transmission in the example is called a parity check code and will detect an odd number of errors, but will not detect an even number of errors.
Example
Consider the matrix
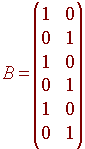
This matrix takes two letter words and produces a 5 letter word. The table for this is
| Message | Transmission |
| (0,0) | (0,0,0,0,0,0) |
| (1,0) | (1,0,1,0,1,0) |
| (0,1) | (0,1,0,1,0,1) |
| (1,1) | (1,1,1,1,1,1) |
Notice that this transmission just repeats the message three times. It will detect one or two errors, hence is called a double-error detecting code. If we assume that there will never be more than one error, then we can correct an error. For example, if the received transmission is (1,1,0,1,0,1), then the only possible correct transmission that gives one error is (1,0,1,0,1,0), hence the original message was (1,0).
Back to the Matrices and Applications Home Page
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions