Linear Systems and Matrices

Linear Systems

An n by n linear system of equations is a system of n linear equations in n variables.

        a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n  =  b₁
        a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n  =  b₂ 
        ...            ...                ...        ...
        a_n1x₁ + a_n2x₂ + ... + a_nnx_n  =  b_n 

Example

Solve

        2x₁ + 3x₂  =  9
         x₁ - 2x₂  =  1

Solution

To solve this we sequentially perform members of the following three operations:

1. Switch two equations.
   
   
2. Multiply an equation by a nonzero constant.
   
   
3. Replace an equation by that equation plus a multiple of the second equation.
   

We have

                                    Switching the two equations
         x₁ - 2x₂  =  1            
        2x₁ + 3x₂  =  9

                                    Replace the 2nd equation with the 2nd equation + (-2)1st equation
         x₁ - 2x₂  =  1          
                7x₂  =  7

                                    Multiply the second equation by 1/7
         x₁ - 2x₂  =  1          
                  x₂  =  1

                                    Replace the 1st equation with the 1st equation + (2)2nd equation

         x₁   =  3          
         x₂  =  1

Matrices

An m by n matrix is an array of numbers with m rows and n columns. 

Example

The matrix below is a 2 by 3 matrix.

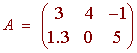
A square matrix is an n by n matrix, that is a matrix such that the number of rows is equal to the number of columns.  The ij^th entry is the number in the i^th row and j^th column.  For example, the the matrix above the 1 2^th entry is

        a₁₂  =  4

Note:  A vector such at <2,4,6> can be looked as a 1 by 3 matrix.  

A square matrix is called a diagonal matrix if 

        a_ij  =  0        for        i  j

The matrix below is a diagonal matrix

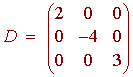
If all the entries of a diagonal matrix are equal, then the matrix is called a scalar matrix.  The example below is a scalar matrix.

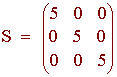
Addition Subtraction and Scalar Multiplication

Just as with vectors we can add and subtract matrices and multiply a matrix by a scalar.  To add or subtract matrices the dimensions of the two matrices must be the same.

Example

Let 

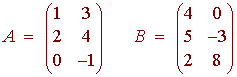
then

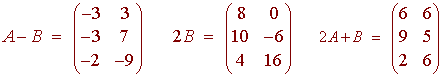
Two matrices are called equal if all of their entries are equal.

If A is an m by n matrix, then the transpose of A, A^T, is the n by m matrix with the rows and columns switched.

        (A^T)_ij  =  A_ji 

In the above example

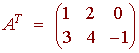
Example of the Theoretical Exercise

Prove that  

        (A^T)^T  =  A

Solution

We have 

        ((A^T)^T )_ij =  (A^T)ji  =  A_ij 

Since the ij^th entries are equal for each ij, the matrices are equal.

Back to the Matrices and Applications Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions