Matrix Multiplication

The Dot Product for Vectors in Rⁿ

Let

        a  =  [a₁ a₂ ... a_n]

 be a vector in Rⁿ (considered as a 1 by n matrix) and let    

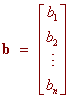
then the dot product of a and b is defined by

        a ^.  b  =  a₁b₁ + a₂b₂ + ... + a_nb_n  = S a_ib_i

Example

Find the dot product of

       a  =  [2  1  0  6  -1]   and    b  =  

Solution

We have

        a ^. b  =  (2)(5) + (1)(2) + (0)(-3) + (6)(0) + (-1)(1)  =  11

Matrix Multiplication

There are many ways of thinking about a matrix.  One way is as a collection of row vectors and another way is as a collection of column vectors.  Consider the m by p matrix A (considered as a matrix of row vectors) and the p by n matrix B (considered as a matrix of column vectors).  The matrices are shown below.

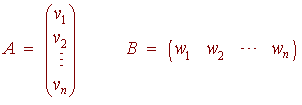
We define the matrix product by

        (AB)_ij  =  v_i . w_j

Remark: If the number of columns of A is not equal to the number of rows of B, then the product AB is not defined.

Remark: It is not true in general that AB and BA are the same matrix even if they are both defined.

We can also define

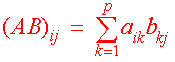
Example

Let

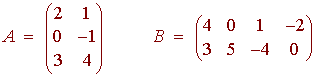
Then the matrix product is

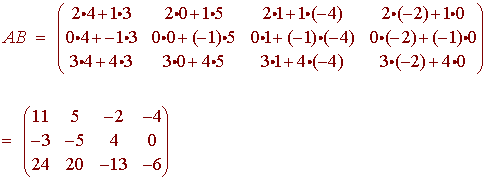
Linear Systems

Any m by n linear system can be written in the form 

        Ax  =  b

Where A is the coefficient matrix, 

        x^T  =  (x₁  x₂  ...  x_n)

and b is the m by 1 matrix of numbers to the left of the equality.  For example the linear system

        2x + 3y + z  =  0
        3x - 4y - z  =  6
        x  + 2y + 3x  =  2

can be written as 

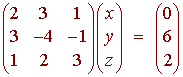
Often, we write the matrix equation in augmented form as shown below

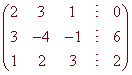
Back to the Matrices and Applications Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions