Properties of Matrix Operations

Properties of Addition

The basic properties of addition for real numbers also hold true for matrices. 

Let A, B and C be m x n matrices

1. A + B  =  B + A    commutative
   
   
2. A + (B + C)  =  (A + B) + C    associative
   
   
3. There is a unique m x n matrix O with
   
           A + O  =  A        additive identity
   
   
4. For any  m x n matrix A there is an m x n matrix B (called -A) with
   
          A + B  =  O        additive inverse

The proofs are all similar.  We will prove the first property.

Proof of Property 1

We have

        (A + B)_ij  =  A_ij + B_ij     definition of addition of matrices

        =  B_ij + A_ij         commutative property of addition for real numbers

       =  (B + A)_ij       definition of addition of matrices

Notice that the zero matrix is different for different m and n.  For example

Properties of Matrix Multiplication

Unlike matrix addition, the properties of multiplication of real numbers do not all generalize to matrices.  Matrices rarely commute even if AB and BA are both defined.  There often is no multiplicative inverse of a matrix, even if the matrix is a square matrix.  There are a few properties of multiplication of real numbers that generalize to matrices.  We state them now.

Let A, B and C be matrices of dimensions such that the following are defined.  Then

1. A(BC)  =  (AB)C                 associative
   
   
2. A(B + C)  =  AB + AC        distributive
   
   
3. (A + B)C  =  AC + BC        distributive
   
   
4. There are unique matrices I_m and I_n with
   
           I_m A  =  A I_n  =  A        multiplicative identity

We will often omit the subscript and write I for the identity matrix.  The identity matrix is a square scalar matrix with 1's along the diagonal.  For example

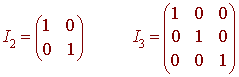
We will prove the second property and leave the rest for you.

Proof of Property 2

Again we show that the general element of the left hand side is the same as the right hand side.  We have

        (A(B + C))_ij  = S(A_ik(B + C)_kj)        definition of matrix multiplication

        =  S(A_ik(B_kj + C_kj))        definition of matrix addition

        =  S(A_ikB_kj + A_ikC_kj)       distributive property of the real numbers

        =  S A_ikB_kj + S A_ikC_kj     commutative property of the real numbers

        =  (AB)_ij + (AC)_ij        definition of matrix multiplication

where the sum is taken from 1 to k.

Example

We will demonstrate property 1 with

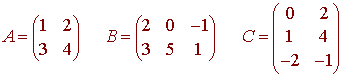
We have

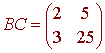
so that

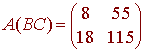
We have

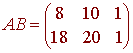
so that

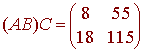
Properties of Scalar Multiplication

Since we can multiply a matrix by a scalar, we can investigate the properties that this multiplication has.  All of the properties of multiplication of real numbers generalize.  In particular, we have

Let r and s be real numbers and A and B be matrices.  Then

1. r(sA)  =  (rs)A
   
     
2. (r + s)A  =  rA + sA
   
   
3. r(A + B)  =  rA + rB
   
   
4. A(rB)  =  r(AB)  =  (rA)B

We will prove property 3 and leave the rest for you.  We have

        (r(A + B))_ij  =  (r)(A + B)_ij          definition of scalar multiplication

        =  (r)(A_ij + B_ij)        definition of addition of matrices

        =  rA_ij + rB_ij        distributive property of the real numbers

        =  (rA)_ij + (rB)_ij        definition of scalar multiplication

        =  (rA + rB)_ij        definition of addition of matrices

Properties of the Transpose of a Matrix

Recall that the transpose of a matrix is the operation of switching rows and columns.  We state the following properties.  We proved the first property in the last section.

Let r be a real number and A and B be matrices.  Then

1. (A^T)^T  =  A
   
   
2. (A + B)^T  =  A^T + B^T
   
   
3. (AB)^T  =  B^TA^T
   
   
4. (rA)^T  =  rA^T

Back to the Matrices and Applications Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions