Math 203 Practice Midterm 2

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.

  Printable Key

Problem 1 

Let  L:  R² --> R³   be a linear transformation such that 

        L (1,4) = (1,-1,3)   and     L (0,2) =  (2,1,4)

Find L(1,0)

  Solution

Problem 2

Of the following two subsets of the vector space of differentiable functions, determine which is a subspace.  For the one that is not a subspace, demonstrate why it is not.  For the one that is a subspace, prove that it is a subspace.

A.  S  =  {f | f(3)  =  f '(3)} 

B.  T  =  {f | f(0)f '(0)  =  0} 

  Solution

Problem 3

Let  S  =  {t², t² + 2t, t² + 3}  and T  =  {2t - 1, 5t - 3, t²} be subsets of P₂ 

A.     Prove that S is a basis for P₂.  

Solution

B.     Find the transition matrix P_S<--T.

Solution

Problem 4  

Prove that if A is an m x n matrix such that the columns of A are linearly independent and the rows of A are linearly independent, then m = n.

Solution

Problem 5 

Let

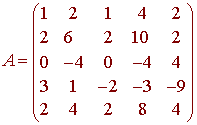
A.     Find the rank and the nullity of A. 

B.     Find a basis for the Null Space of A.

C.     Find a basis for the Column Space of A using columns of A.

D.     Find a basis for the Row Space of A using rows of A.

Solution

Problem 6

Let  S  =  {v₁, v₂, ..., v_n} be a set of linearly independent vectors and let v be a vector in the span of S.  Prove that v can uniquely be written as a linear combination of elements of S.  That is that prove that if

      v  =  a₁v₁ +a₂v₂ + ... + a_nv_n        and        v  =  b₁v₁ +b₂v₂ + ... + b_nv_n     

then

        a₁  =  b₂, a₂  =  b₂, ... , a_n  =  b_n

Solution

Problem 7 

Let S = {u₁, u₂, ... ,u_n} be an orthonormal set in Rⁿ, and let A be the matrix whose j^th column is u_j.  Show that det(A) is not equal to zero.

Solution