Math 203 Practice Exam 2

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.  Do your work on your own paper.

  Printable Key

Problem 1

Let  S  =  {t2, t2 + 2t, t2 + 3}  and T  =  {2t - 1, 5t - 3, t2} be subsets of P2 

A.     Prove that S is a basis for P2.  

B.     Find the change of basis matrix PS<--T.

   

Problem 2

Of the following two subsets of the vector space of differentiable functions, determine which is a subspace.  For the one that is not a subspace, demonstrate why it is not.  For the one that is a subspace, prove that it is a subspace.

A.  S  =  {f | f(3)  =  f '(3)} 

B.  T  =  {f | f(0)f '(0)  =  0} 

 

Problem 3

Let V be the subspace of differentiable functions spanned by {ex, e2x, e3x} and let

        L:  V --->  V

be the linear transformation with 

        L(f(x))  =  f ''(x) - 3f '(x) + 2f(x)

 

A.     Write down the matrix AL with respect to the given basis.

B.     Find the a basis for the kernel and range of L.

 

Problem 4 

Let W = Span{(1,1,0,1), (0,1,2,3)}.  Find a basis for the orthogonal complement of W.

Problem 5
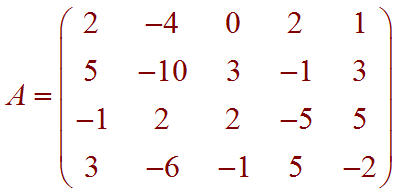
Let A=Matrix Rows: (2,-4,0,2,1)(5,-10,3,-1,3)(-1,2,2,-5,5)(3,-6,-1,5,-2)
Find the following:

  1. A basis for the column  space of A.

  2. A basis for the row space of A.

  3. A basis for the null space of A.

  4. The nullity of A.

  5. The rank of A.

   

Problem 6

Let  L:  V ---> V  be a linear transformation.  Use the fact that 

        dim(Ker L) + dim(Range L)  =  dim(V)

to show that if L is one to one then L is onto. 

Problem 7 

Let A and B be matrices and let v be an eigenvector of both A and B.  Prove that v is an eigenvector of the product AB.

Problem 8
Without the use of a calculator, diagonalize the matrix
  
A = Matrix[ (2,6),(6,7)]

Problem 9

Answer True of False and explain your reasoning.

 

A.    Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors.  Then

         

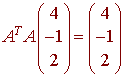
B.  If A is an mxn matrix such that the rows of A and the columns of A are both linear independent sets, then n = m.

C.  If u and v are eigenvectors for a matrix A, then u + v is also an eigenvector for A.

D.  If A is similar to B and B is similar to C, then A is similar to C.

E.  If l is an eigenvalue for A, then l2 is an eigenvalue for A2.

F.  The vectors (1,1,0), (1,0,1), and (0,0,1) are a basis for P2.