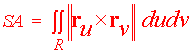Parametric Surfaces
Definition of a Parametric Surface
We have now seen many kinds of functions. When we talked about parametric curves, we defined them as functions from R to R2 (plane curves) or R to R3 (space curves). Because each of these has its domain R, they are one dimensional (you can only go forward or backward). In this section, we investigate how to parameterize two dimensional surfaces. Below is the definition.
|
Definition of Parametric Surfaces A parametric surface is a function with domain R2 and range R3. |
Remark: We typically use the variables u and v for the domain and x, y, and z for the range. We often use vector notation to exhibit parametric surfaces.
Example
A sphere of radius 7 can be parameterized by
r(u,v) = 7cos u sin v i + 7sin u sin v j + 7 cos v k
Notice that we have just used spherical coordinates with the radius held at 7.
We can use a computer to graph a parametric surface. Below is the graph of the surface
r(u,v) = sin u i + cos v j + exp(2u1/3 + 2v1/3) k
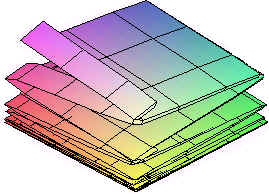
Example
Represent the surface
z = ex cos(x - y)
parametrically
Solution
The idea is similar to parametric curves. We just let x = u and y = v, to get
r(u,v) = u i + v j + eu cos(u - v) k
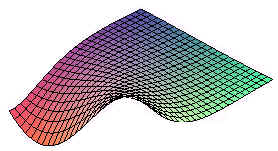
Example
A surface is created by revolving the curve
y = cos x
about the x-axis. Find parametric equations for this surface.
Solution
For a fixed value of x, we get a circle of radius cos x. Now use polar coordinates (in the yz-plane) to get
r(u,v) = u i + r cos v j + r sin v k
Since u = x and r = cos x, we can substitute cos u for r in the above equation to get
r(u,v) = u i + cos u cos v j + cos u sin v k
Normal Vectors and Tangent Planes
We have already learned how to find a normal vector of a surface that is presented as a function of two variables, namely find the gradient vector. To find the normal vector to a surface r(u,v) that is defined parametrically, we proceed as follows.
The partial derivatives
ru(u0,v0) and rv(u0,v0)
will lie on the tangent plane to the surface at the point (u0,v0). This is true, because fixing one variable constant and letting the other vary, produced a curve on the surface through (u0,v0). ru(u0,v0) will be tangent to this curve. The tangent plane contains all vectors tangent to curves passing through the point.
To find a normal vector, we just cross the two tangent vectors.
Example
Find the equation of the tangent plane to the surface
r(u,v) = (u2 - v2) i + (u + v) j + (uv) k
at the point (1,2).
Solution
We have
ru(u,v) = (2u) i + j + v k
rv(u,v) = (-2v) i + j + u k
so that
ru(1,2) = 2 i + j + 2 k
rv(1,2) = -4 i + j + k
r(1,2) = -3 i + 3 j + 2 k
Now cross these vectors together to get
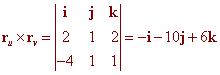
We now have the normal vector and a point (-3,3,2). We use the normal vector-point equation for a plane
-1(x + 3) - 10(y - 3) + 6(z - 2) = 0
-x - 10y + 6z = -15 or x + 10y - 6z = 15
Surface Area
To find the surface area of a parametrically defined surface, we proceed in a similar way as in the case as a surface defined by a function. Instead of projecting down to the region in the xy-plane, we project back to a region in the uv-plane. We cut the region into small rectangles which map approximately to small parallelograms with adjacent defining vectors ru and rv. The area of these parallelograms will equal the magnitude of the cross product of ru and rv. Finally add the areas up and take the limit as the rectangles get small. This will produce a double integral.
|
Area of a Parametric Surface Let S be a smooth surface defined parametrically by r(u,v) = x(u,v) i + y(u,v) j + z(u,v) k where u and v are contained in a region R. Then the surface area of S is given by
|
Since the magnitude of a cross product involves a square root, the integral in the surface area formula is usually impossible or nearly impossible to evaluate without power series or by approximation techniques.
Example
Find the surface area of the surface given by
r(u,v) = (v2) i + (u - v) j + (u2) k 0 < u < 2 1 < v < 4
Solution
We calculate
ru(u,v) = j + 2u k
rv(u,v) = (2v) i - j
The cross product is
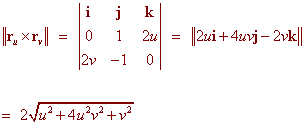
The surface area formula gives
![]()
This integral is probably impossible to compute exactly. Instead, a calculator can be used to obtain a surface area of 70.9.
Back to the Vector Fields and Vector Integration Home Page
Back to the Vector Calculus Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions