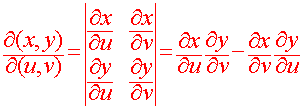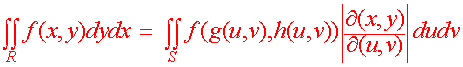Jacobians
Review of the Idea of Substitution
Consider the integral
![]()
To evaluate this integral we use the u-substitution
u = x2
This substitution sends the interval [0,2] onto the interval [0,4]. We can see that there is stretching of the interval. The stretching is not uniform. In fact, the first part [0,0.5] is actually contracted. This is the reason why we need to find du.
du
dx 1
= 2x or
=
dx
du 2x
This is the factor that needs to be multiplied in when we perform the substitution. Notice for small positive values of x, this factor is greater than 1 and for large values of x, the factor is smaller than 1. This is how the stretching and contracting is accounted for.
We have seen that when we convert to polar coordinates, we use
dydx = rdrdq
With a geometrical argument, we showed why the "extra r" is included. Taking the analogy from the one variable case, the transformation to polar coordinates produces stretching and contracting. The "extra r" takes care of this stretching and contracting. The goal for this section is to be able to find the "extra factor" for a more general transformation. We call this "extra factor" the Jacobian of the transformation. We can find it by taking the determinant of the two by two matrix of partial derivatives.
|
Definition of the Jacobian Let x = g(u,v) and y = h(u,v) be a transformation of the plane. Then the Jacobian of this transformation is
|
Example
Find the Jacobian of the polar coordinates transformation
x(r,q) = r cos q y(r,q) = r sin q
Solution
We have
![]()
This is comforting since it agrees with the extra factor in integration.
Double Integration and the Jacobian
|
Theorem: Integration and Coordinate Transformations Let
given by x = g(u,v), y = h(u,v) be a transformation on the plane that is one to one from a region S to a region R. If g and h have continuous partial derivatives such that the Jacobian is never zero, then
|
Remark: A useful fact is that the Jacobian of the inverse transformation is the reciprocal of the Jacobian of the original transformation.
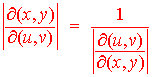
This is a consequence of the fact that the determinant of the inverse of a matrix A is the reciprocal of the determinant of A.
Idea of the Proof
As usual, we cut S up into tiny rectangles so that the image under T of each rectangle is a parallelogram.
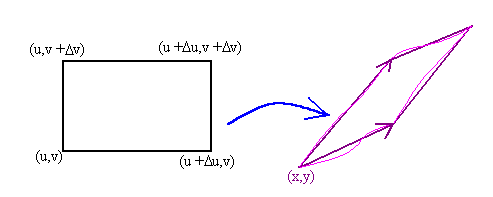
We need to find the area of the parallelogram. Considering differentials, we have
T(u + Du,v) @ T(u,v) + (xuDu,yuDu)
T(u,v + Dv) @ T(u,v) + (xvDv,yvDv)
Thus the two vectors that make the parallelogram are
P = guDu i + huDu j
Q = gvDv i + hvDv j
To find the area of this parallelogram we just cross the two vectors.
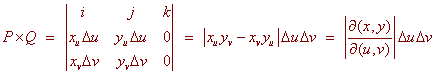
and the extra factor is revealed.
Example
Use an appropriate change of variables to find the volume of the region below
z = (x - y)2
above the x-axis, over the parallelogram with vertices (0,0), (1,1), (2,0), and (1,-1)
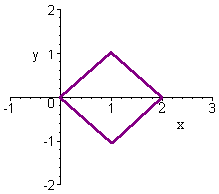
Solution
We find the equations of the four lines that make the parallelogram to be
y = x y = x - 2 y = -x y = -x + 2
or
x - y = 0 x - y = 2 x + y = 0 x + y = 2
The region is given by
0 < x - y < 2 and 0 < x + y < 2
This leads us to the inverse transformation
u(x,y) = x - y v(x,y) = x + y
The Jacobian of the inverse transformation is
![]()
Since the Jacobian is the reciprocal of the inverse Jacobian we get
![]()
The region is given by
0 < u < 2 and 0 < v < 2
and the function is given by
z = u2
Putting this all together, we get the double integral
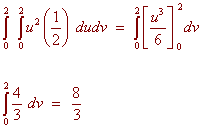
Jacobians and Triple Integrals
For transformations from R3 to R3, we define the Jacobian in a similar way
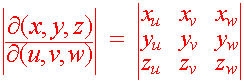
Example
Find the Jacobian for the spherical coordinate transformation
x = r cosq sinf y = r sinq sinf z = r cosf
Solution
We take partial derivatives and compute

Back to the Multiple Integration Home Page
Back to the Vector Calculus Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions