Double Integrals and Volume

Double Riemann Sums

In first year calculus, the definite integral was defined as a Riemann sum that gave the area under a curve.  There is a similar definition for the volume of a region below a function of two variables.  Let f(x,y) be a positive function of two variables and consider the solid that is bounded below by f(x,y) and above a region R in the xy-plane.  

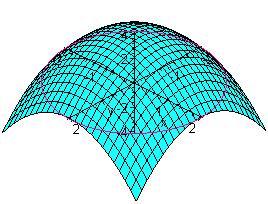
For a two dimensional region, we approximated the area by adding up the areas of many approximating rectangles.  For the volume of a three dimensional solid, we take a similar approach.  Instead of rectangles, we use rectangular solids for the approximation.  We cut the region R into rectangles by drawing vertical and horizontal lines in the xy-plane.  Rectangles will be formed.  We let the rectangles be the base of the solid, while the height is the z-coordinate of the lower left vertex.  One such rectangular solid is shown in the figure.  

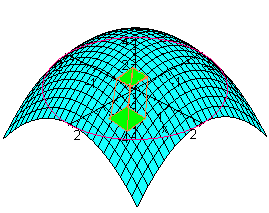
Taking the limit as the rectangle size approaches zero (and the number of rectangles approaches infinity) will give the volume of the solid.  If we fix a value of x and look at the rectangular solids that contain this x, the union of the solids will be a solid with constant width Dx.  The face will be approximately equal to the area in the yz-plane of the (one variable since x is held constant) function  z  =  f(x,y).  

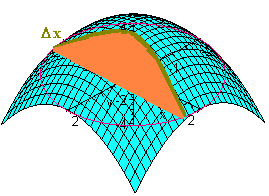
This area is equal to 

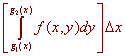
If we add up all these slices and take the limit as Dx approaches zero, we get

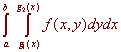
Which is just the double integral defined in the last section

Instead of fixing the variable x we could have held y constant.  The picture below illustrates the resulting wedge.

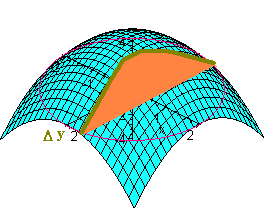
By a similar argument, the volume of the wedge is 

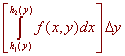
Adding up all the wedge areas gives the total volume

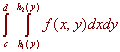
This shows that the volume is equal to the iterated integral no matter which we integrate first.  This is called Fubini's Theorem.  Technically the volume is defined as the double Riemann sum of f(x,y) where we sum over the partition of R in the xy-plane.  We state it below.

Notice that all the typical properties of the double integral hold.  For example, constants can be pulled out and the double integral of the sum of two functions is the sum of the double integrals of each function.

Finding Volume

Example

Set up the integral to find the volume of the solid that lies below the cone

and above the xy-plane.  

Solution

The cone is sketched below

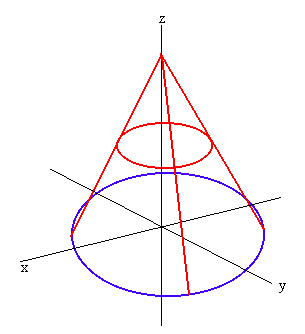
We can see that the region R is the blue circle in the xy-plane.  We can find the equation by setting z  =  0.

Solving for y (by moving the square root to the left hand side,  squaring both sides, etc) gives

The "-" gives the lower limit and the "+" gives the upper limit.  For the outer limits, we can see that 

        -4  <  x  <  4

Putting this all together gives

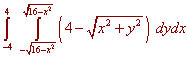
Either by hand or by machine we can obtain the result 

        Volume  =  64 p/3

Notice that this agrees with the formula 

        Volume  =  p r²h/3

Exercise

Set up the double integral for this problem with dxdy instead of dydx.  Then show that the two integrals give the same result.

Example

Set up the double integral that gives the volume of the solid that lies below the sphere

        x² + y² + z²  =  6

and above the paraboloid 

        z  =  x² + y² 

Solution

The picture below indicated that the region is the disk that lies inside that circle of intersection of the two surfaces.  We substitute

        x² + y² + (x² + y²)²  =  6

or

        x² + y² + (x² + y²)² - 6  =  0

Now factor with x² + y² as the variable to get

        (x² + y² - 2)(x² + y² + 3)  =  0

The second factor has no solution, while the first is 

        x² + y²  =  2

Solving for y gives

and

        -  <  x  < 

Just as we did in one variable calculus, the volume between two surfaces is the double integral of the top surface minus the bottom surface.  We have

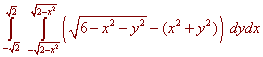
Again we can perform this integral by hand or by machine and get

        Volume  =  7.74

Back to the Multiple Integration Home Page

Back to the Vector Calculus Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions