Math 202 Practice Final
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your Work
Problem 1 Please answer the following true or false. If false, explain why or provide a counter example. If true, explain why.
A. Let Q be a three dimensional solid and let
F(x,y,z) = (x2y + sin z)i+ (cos x - xy2)j + (3xy + z)k
and let S be the boundary of Q with outwardly pointing normal. The the volume so Q is given by
![]()
B. Let F = 3xy i + cosx j and let C1 and C2 be as shown below. Then
![]()
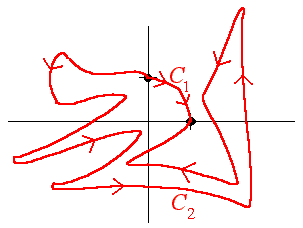
C. A new particle, the fluxon, has been discovered to be emitted from the sun. The particle emits a force field
F(x,y,z) = (y2 - z) i + (x2 - z) j + (x2 + y2) k
where the origin represents the center of the sun. If the total flux through the earth's northern hemisphere has been calculated as 10,000, then the total flux through the earth's southern hemisphere must also be 10,000.
Problem 2 You are the captain of the spaceship Potential that you have programmed to follow the vector-valued function
r(t) = (t2 + 5) i + (t - 3) j + t3 k
where t is measured in hours. However, at time t = 2, your engines fail and your ship begins drifting in deep space. There is a deep space station located at (6,2,38).
A. Find the vector-valued function that describes the Potential's flight after the engines failed. Use t = 2 to represent the time at which your engines first shut down. (Hint: This should be a linear vector valued function.)
B. Will your ship make it to the station, or will you float helplessly for eternity?
Problem 3 Show that the helix
r(t) = (R cos t) i + (R sin t) j + t k
where R is a positive constant, has the property that N(t) . r(t) is a constant. Find this constant.
Problem 4 The probability density function for an event is given by
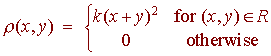
where R is the square with vertices (4,0), (6,2), (4,4), and (2,2).
A. Use the appropriate change of variables (Jacobians) to find k that is solve
![]()
B. Find the probability that 0 < x - y < 1
Problem 5 Switch the order of integration and write as one double integral

Problem 6 Set up the integrals that give the following. Use the most appropriate coordinate system.
A. The mass of the solid that lies inside the sphere
x2 + y2 + z2 = 9
and outside the cone
z2 = x2 + y2
that has density function
![]()
B. The surface area of the part of the paraboloid
z = x2 + y2
that lies inside the cylinder
x2 + y2 = 4
Problem 7 Find the work done by the force field
F(x,y) = (3x2 - y) i + (x2 - y3) j
as a particle moves counterclockwise around the rectangle with vertices (2,1), (5,1), (5,5), and (2,5).
Problem 8
Verify Stokes Theorem where
F(x,y,z) = (2x) i + (2y) j + (z sin z3) k
and S is part of the paraboloid
z = 9 - x2 - y2
that lies above the plane z = 8 oriented upward.
Problem 9
Use the transformations
S(u,v,w): x(u,v,w) = u - v + w, y(u,v) = v+w, z(u,v,w) = 2w
and
T(u,v,w): u(r,s,t) = rsin(s)cos(t), v(r,s,t) = rsin(s)sin(t), w(r,s,t) = rcos(s)
To represent the volume of the solid inside of
(x + y - z)2 + (y - z/2)2 + (z/2)2 = 4
as a triple integral with constants for all the bounds.