MATH
202 PRACTICE MIDTERM 2
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
PROBLEM 1
Please answer the following true or false.
If false, explain why or provide a counter example.
If true explain why.
A)
If all six limits of integration of an
integral written in spherical coordinates are constants, then the region of
integration is a sphere.
False, it can be a part of a sphere. For example

represents a cone with a rounded top.
B)

False,
the integrands work out when you convert, but the regions are different.
The left side is the part of the sphere of radius 9 inside the cylinder of
radius 3 and the right side is a cone.
PROBLEM 2 Set up
integrals to evaluate the following. Use
the coordinate system that will most effectively solve the integral.
A.
The mass of the tetrahedron that lies in the first octant and below the
plane x + y + 2z = 2
such that the density function is f(x,y,z)
= 3yz
.
The tetrahedron is pictured below. We find the triple integral (using dzdydx) The bottom is z = 0 and the top is
z
= 2 - .5(x + y)
To find the outer limits we draw the projection of the surface on the xy-plane as shown to the right. The bottom curve is y = 0 and the top curve is y = -x + 2. The farthest to the left that x gets is 0 and the farthest to the right is 2. Putting this together, we get

B.
The surface area of the part of the paraboloid
z = 9 - x2 - y2
that lies above the plane
z = 5
.
plane
z = 5
.
The picture is shown to the right. We can use polar coordinates to simplify the region which is a circle of radius 2 since solving
9 - r2 = 5
gives r = 2.
The paraboloid becomes. We have
zx = -2x zy = -2y
so that
1 + zx2 + zy2 = 1 + 4x2 + 4y2 = 1 + 4r2
Putting this all together gives
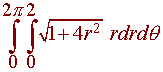
C.
The moment of inertia about the z-axis of the solid between the cylinders
x2 + y2 = 25
and
x2
+ z2 = 25 that has density function 1.
r = 5 and r2cos2 q + z2 = 25
the inner limits are
![]()
The outer limits just come from the circle of radius 5. The integrand is
x2 + y2 = r2 r = r3
Putting this together gives

PROBLEM 3
Switch the
order of integration. 

The key to this problem is to graph the region and notice that to integrate with dxdy we must break the region into two pieces. As shown to the right. We get

PROBLEM 4
A master dart
thrower has determined that her probability density function is inversely
proportional to one more than the fourth power of the distance in centimeters
from the center of the dartboard.
We integrate

by transforming to polar coordinates. We get

To integrate this we can use u-substitution with
u = r2 du = 2r dr
This gives

Since the probability must be equal to one, the constant of proportionality must be the reciprocal of this double integral that is
2
k =
p2
B. Find the probability of her hitting the bullís-eye which is one centimeter in radius.
We work the same problem except that the region of integration is the circle of radius 1 and we include the constant of proportionality. We have

PROBLEM 5
Consider the solid described by
(x + 2y)2 + (2y - 2z)2 + (x + z)2
< 25
with density function
f(x,y) = x + 2y
Show that the mass of the solid is equal to

Hint:
Recall that

We use Jacobians with
u = x + 2y v = 2y+2z w = x + z
We have

Thus the Jacobian is 1/6. The function f becomes u. The region becomes
u2 + v2 + w2 < 25
which is a sphere of radius 5. The result follows when we put this region in spherical coordinates (using (u,v,w) instead of (x,y,z)).
