Probability

Probability

For an experiment we define an event to be any collection of possible outcomes.     

A simple event is an event that consists of exactly one outcome.  

    or:  means the union i.e.  either can occur

    and:  means intersection i.e. both must occur

Two events are mutually exclusive if they cannot occur simultaneously.  

For a Venn diagram, we can tell that two events are mutually exclusive if their regions do not intersect

We define Probability  of an event E to be to be 

number of simple  events within E P(E)  =                                                                              total number of possible outcomes

We have the following:

1. P(E) is always between 0 and 1.
   
   
2. The sum of the probabilities of all simple events must be 1.
   
   
3. P(E) + P(not E) = 1
   
   
4. If E and F are mutually exclusive then 
   
           P(E or F) = P(E) + P(F)

The Difference Between And and Or

If E and F are events then we use the terminology

        E and F 

to mean all outcomes that belong to both E and F

We use the terminology

        E Or F 

to mean all outcomes that belong to either E or F.

Example

Below is an example of two sets, A and B, graphed in a Venn diagram.  

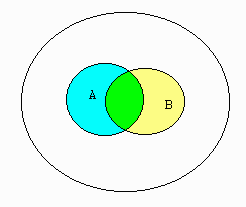
The green area represents A and B while all areas with color represent A or B

Example

    Our Women's Volleyball team is recruiting for new members.  Suppose that a person inquires about the team.

        Let E be the event that the person is female

        Let F be the event that the person is a student

then E And F represents the qualifications for being a member of the team.  Note that E Or F is not enough.

    We define

Definition of Conditional Probability                          P(E and F)         P(E|F) =                                                       P(F)

We read the left hand side as 

        "The probability of event E given event F"

We call two events  independent if

For Independent Events P(E|F)  =  P(E)

Equivalently, we can say that E and F are independent if

For Independent Events P(E and F)  =  P(E)P(F)

Example

    Consider rolling two dice.  Let 

            E be the event that the first die is a 3.

            F be the event that the sum of the dice is an 8.

    Then E and F means that we rolled a three and then we rolled a 5

    This probability is 1/36 since there are 36 possible pairs and only one of them is (3,5)

    We have 

            P(E)  =  1/6  

    And note that (2,6),(3,5),(4,4),(5,3), and (6,2) give F

    Hence 

            P(F)  =  5/36

    We have 

            P(E) P(F) = (1/6) (5/36) 

    which is not 1/36.  

    We can conclude that E and F are not independent.

Exercise

    Test the following two events for independence:

    E the event that the first die is a 1.

    F the event that the sum is a 7.

Hold your mouse over the yellow rectangle for the answer.

A Counting Rule

For two events, E and F, we always have

        P(E or F)  =  P(E) + P(F) - P(E and F)

Example

Find the probability of selecting either a heart or a face card from a 52 card deck.

Solution

We let

        E  =  the event that a heart is selected 

        F  =  the event that a face card is selected

then 

        P(E)  =  1/4        and         P(F)  =  3/13   (Jack, Queen, or King out of 13 choices)

        P(E and F)  =  3/52

The formula gives

        P(E or F)  =  1/4 + 3/13 - 3/52  =  22/52 =  42%

Back to the Probability Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions