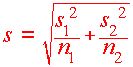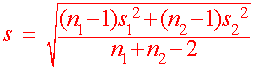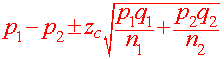Estimating Differences
Difference Between Means
I surveyed 50 people from a poor area of town and 70 people from an affluent
area of town about their feelings towards minorities. I counted the
number of negative comments made. I was interested in comparing their
attitudes. The average number of negative
comments in the poor area was 14 and in the affluent area was
12. The
standard deviations were 5 and 4 respectively.
Let's determine a 95% confidence for the difference
in mean negative comments. First, we need some formulas.
|
Theorem The distribution of the difference of means
x1 -
x2
has mean
|
For our investigation, we use s1 and s2 as point estimates for s1 and s2. We have
x1 = 14 x2 = 12 s1 = 5 s2 = 4 n1 = 50 n2 = 70
Now calculate
x1 - x2 = 14 - 12 = 2
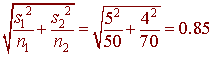
The margin of error is
E = zcs = (1.96)(0.85) = 1.7
The confidence interval is
2 ![]() 1.7
1.7
or
[0.3, 3.7]
We can conclude that the mean difference between the number of racial slurs that
poor and wealthy people make is between 0.3 and 3.7.
Note: To calculate the degrees of freedom, we can take the smaller of the two numbers n1 - 1 and n2 - 1. So in the prior example, a better estimate would use 49 degrees of freedom. The t-table gives a value of 2.014 for the t.95 value and the margin of error is
E = tcs = (2.014)(0.85) = 1.7119
which still rounds to 1.7. This is an example that demonstrates that using the t-table and z-table for large samples results in practically the same results.
Small Samples With Pooled Pooled Standard Deviations (Optional)
When the sample size is small, we can still run the statistics provided the distributions are approximately normal. If in addition we know that the two standard deviations are approximately equal, then we can pool the data together to produce a pooled standard deviation. We have the following theorem.
|
Pooled Estimate of s
with n1 + n2 - 2 degrees of freedom |
You've gotta love the beautiful formula!
Note
After finding the pooled estimate we have that a confidence interval is given by
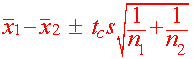
Example
What is the difference between commuting patterns for students and professors. 11 students and 14 professors took part in a study to find mean commuting distances. The mean number of miles traveled by students was 5.6 and the standard deviation was 2.8. The mean number of miles traveled by professors was 14.3 and the standard deviation was 9.1. Construct a 95% confidence interval for the difference between the means. What assumption have we made?
Solution
We have
x1 = 5.6 x2 = 14.3 s1 = 2.8 s2 = 9.1 n1 = 11 n2 = 14
The pooled standard deviation is
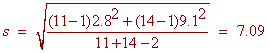
The point estimate for the mean is
14.3 - 5.6 = 8.7
and
![]()
Use the t-table to find tc for a 95% confidence interval with 23 degrees of freedom and find
tc = 2.07
8.7 ![]() (2.07)(7.09)(.403) = 8.7
(2.07)(7.09)(.403) = 8.7 ![]() 5.9
5.9
The range of values is [2.8, 14.6]
The difference in average miles driven by students and professors is between 2.8 and 14.6. We have assumed that the standard deviations are approximately equal and the two distributions are approximately normal.
Difference Between Proportions
So far, we have discussed the difference between two means (both large and small samples). Our next task is to estimate the difference between two proportions. We have the following theorem
And a confidence interval for the difference of proportions is
|
Confidence Interval for the difference of Proportions
|
Note: in order for this to be valid, we need all four of the quantities
p1n1 p2n2 q1n1 q2n2
to be greater than 5.
Example
300 men and 400 women we asked how they felt about taxing Internet sales. 75 of the men and 90 of the women agreed with having a tax. Find a confidence interval for the difference in proportions.
Solution
We have
p1 = 75/300 = .25 q1 = .75 n1 = 300
p2 = 90/400 = .225 q2 = .775 n2 = 400
We can calculate
![]()
We can conclude that the difference in opinions is between -8.5% and 3.5%.
Back to the Estimation Home Page
Back to the Elementary Statistics (Math 201) Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions