Subtracting Whole Numbers
-
No Borrowing
To subtract whole numbers we write them as in an addition problem and subtract each digit moving from the right to the left.
Example:
789
- 34 Note that 9 - 4 = 5, 8 - 3 = 5, and 7 - 0 = 7
755
-
Borrowing is Necessary
If when subtracting digits, the top number is smaller than the bottom, borrowing becomes necessary. We borrow one from the digit to the left.
Example:
Find 41 - 9
Solution
3
4 11
- 9 We have written 41 as 30 + 11. Notice the three in the new tens digit.
32
Example:
Find 1042 - 578
Solution
0 9 14 First we write 52 as 40 + 12. Then notice that 0 can not be borrowed from,
1 0 512
- 5 7 8 so we go to the next digit and write 104 as 90 + 14.
47 4
-
Checking Your Work
We can think of subtraction as the reverse of addition.
Example
To check that 41 - 9 = 32, we can work out 32 + 9:
1
32
+ 9 Since 2 + 9 = 11, we have carried the 1.
41
Exercise
Check your work on the second example: 1052 - 578 = 474
-
Solving for x
We can use this idea that subtraction is the inverse of addition when we answer questions that ask to solve for x:
Example
Solve for x if
15 = x + 11
Solution
We write the reverse of the addition problem which is a subtraction problem. We have
x = 15 - 11
15
- 11 Since 2 + 9 = 11, we have carried the 1.
4
-
Applications
Example
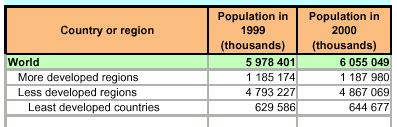
Consider the following table taken for the United Nations world population figures
(http://www.un.org/esa/population/pubsarchive/pop1999-00/pop1999-00.pdf)
-
How much did the world's total population increase between 1999 and 2000?
-
In the year 2000, how many more people were there in less developed countries vs. more developed countries?
-
In the year 1999, how many more people were there in more developed countries vs. the least developed countries?
Solution
We subtract the two world populations:
5 9 14 14
6, 0 5 5, 10 4 9, 0 0 0
- 5, 9 7 8, 4 0 1, 0 0 0 Since the numbers are in thousands, we tag on three 0's
7 6, 6 4 8, 0 0 0
Between 1999 and 2000, the world population increased by 76,648,000 poeple.
We subtract the more developed number from the less developed number
15 16 9
4, 8 6 7, 0 16 9, 0 0 0
- 1, 1 8 7, 9 8 0, 0 0 0 Since the numbers are in thousands, we tag on three 0's
3, 6 7 9, 0 8 9, 0 0 0
In 2000, there were 3,679,089,000 more people in less developed countries than in more developed countries.
We subtract the least developed number from the more developed number
3 14 5
6 4 4, 6 17 7, 0 0 0
- 6 2 9, 5 8 6, 0 0 0 Since the numbers are in thousands, we tag on three 0's
1 5, 0 9 1, 0 0 0
In 1999, there were 15,091,000 more people in more developed countries than in the least developed countries.
-