Function Algebra and Important Functions

I.  Homework

II.   Function notation

We write f(x) to mean the function whose input is x.

Examples:

If f(x) = 2x-3

then f(4) = 2(4) - 3 = 5

We can think of f and the function that takes the input multiplies it by 2 and subtracts 3.  Sometimes it is convenient to write f(x) without the x. Thus:

f( ) = 2( ) - 3

whatever is in the parentheses, we put inside.  For example:

f(x - 1) = 2(x - 1) - 3

(f(x + 4) - f(x))/4 =  ([2(x + 4) - 3] - [2(x) - 3]/4 = (2x + 8 - 3 - 2x + 3)/4 = 8/4 = 2

We will try other examples.

III.  Composition of functions

If f(x) and g(x) are functions then we define f o g (x) as f(g(x))

Example:

If f(x) = 4/x and g(x) = x² - x

The f o g(x) = 4/(x² - x)

IV.  Function Arithmetic

We define the sum, difference, product and quotient of functions in the obvious way.

Example:

If f(x) = (x + 1)/(x - 1) and g(x) = x² + 4

then

(f + g)(x) = (x + 1)/(x - 1)  + (x² + 4)

(f - g)(x) = (x + 1)/(x - 1)  - (x² + 4)

(f g)(x) = [(x + 1)/(x - 1)][(x² + 4)]

(f /g)(x) = [(x + 1)/(x - 1) ]/ (x² + 4)

V.  Four Important Functions.

Section 11.3 discusses four important functions and their variations.  A list is given below:

1)  Linear Functions (lines)

You can identify a linear function as

f(x) = mx + b

their graphs can be found by plotting the y intercept and using the slope to plot the second point.  A demonstration will be given in class.

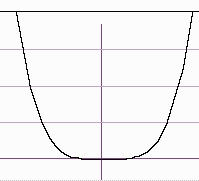
 2)  Quadratic functions (parabolas)

You can identify a quadratic function by the equation

f(x) = ax² + bx + c

Their pictures are parabolas.  In section 9.2, we discussed how to graph a parabola in-depth. 

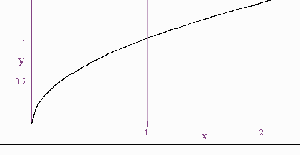
3)  Square root functions:

You can identify a square root function by the equation

f(x) = sqrt(x)

They are half parabolas on their sides.

4)  Absolute Value functions:

You can identify  an absolute value function by the equation

y = |x|.

These look like the letter "V".

VI.  Polynomials

A polynomial  function is a sum of multiples of powers of x.  Examples are

f(x) = 3x⁴ - 2x³ +  x² - 3

Their graphs are beyond the scope of this course.   Other examples will be given.

VII.  Graphing basic functions:

To graph a square root function we plot enough points and connect the dots making sure the shape works with the given basic shape.  

Examples will be given in class.