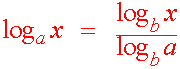Log Bases and Log equations

The Common Logarithm

In chemistry, base 10 is the most important base.  We write

        log x 

to mean the log base ten of x.  

Example:  

        log 10,000,000  =  log 10⁷  =  7 

and 

        log 0.00000001  =  log 10^-8  

Example

We can see that 

        log 12,343,245 

is between 7 and 8 since

        10,000,000  <  12,343,245  <  100,000,000

        log 10,000,000  =  7 

and 

        log 100,000,000  =  8

Example

We can see that 

        log 0.0000145 

is between -5 and -4 since

        0.00001  <  0.0000145  <  0.0001 

and

        log 0.00001  =  -5 

and 

        log 0.0001  =  -4

Exercise

Use your calculator to find

        log 1,234           

and 

        log 0.00234       

Change of base formula

We next want to be able to use our calculator to evaluate a logarithm of any base.  Since our calculator can only evaluate bases e and 10, we want to be able to change the base to one of these when needed.  The formula below is what we need to accomplish this task.

 

Change of Base Formula

Proof

We write 

        y   =    log_a x

So that 

        a^y   =   x

Take  log_b of both sides we get

        log_b a^y   =   log_b x

Using the power rule:

        y log_b a  =  log_b x

Dividing by  log_b a

                   log_b x
        y  =                  
                   log_b a

Example

Find  

        log₂ 7

We have

                         log 7
        log₂ 7  =                =  2.807...
                         log 2

Log Equations 

Example

Solve 

        log₂ x - log₂ (x - 2) - 3  =  0

We use the following step by step procedure:

Step 1:  bring all the logs on the same side of the equation and everything else on the other side.

        log₂ x - log₂(x - 2)  =  3

Step 2:  Use the log rules to contract to one log

                    x
        log₂              =  3
                  x - 2

Step 3:  Exponentiate to cancel the log (run the hook).

               x
                        =  2³  =  8
            x - 2

Step 4:  Solve for x

        x  =  8(x - 2)  =  8x - 16

        7x = 16

                 16
        x =             
                  7

Step 5:  Check your answer

        log₂ (16/7) - log₂ (16/7 - 2)  =  3

Exercises:  

1. log(x + 2) - log(x - 1) = 1       
   
   
   

2. log₂(x) + log₂(x + 5)  = 2       

 Exponential Equations

Example

Solve for x in 

        2^{x - 1}  = 3^{x + 1}  

Step 1:  Take logs of both sides using one of the given bases

        log₂ 2^{x - 1}  =  log₂ 3^{x + 1}  

Step 2:  Use the log rules to simplify

        x - 1  =  (x + 1) log₂ 3  =  (x + 1)(log 3)/(log2)  =  1.58(x + 1)

Step 3:  Solve for x

        x - 1  =  1.58 x + 1.58

        -.58 x  =  2.58

        x  =  -4.45

Step 4:  Check your answer.

Exercises

1. 3^{x - 2}  =  5^{2x  - 3}  
   
   
   
   

2. 2^{1 - x}   =  3^{x - 1}  
   
   

For an interactive computer lesson on exponential equations click here

or to play the log memory game click here 

Back to the Exponentials and Logs Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions