Practice Midterm II

Name

MATH 154 PRACTICE MIDTERM II

Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Do all your work and give all your answers on you own sheet of paper. Show your work.

Problem 1

Solve the following:

A. (10 Points) log₆(x - 5) + log₆(x) = 2

Solution

Use the sum to product rule of logarithms

log₆[(x)(x - 5)] = 2

(x)(x - 5) = 6² Remember logs are exponents

x² - 5x = 36 Multiplying out

x² - 5x - 36 = 0 Subtracting 36 from both sides

(x - 9)(x + 4) = 0

x = 9 or x = 4

Notice that 4 is not a solution since it is not in the domain of log₆(x - 5). 9 is a solution, as you can verify with your calculator.

B. (10 Points) 2^2x-1 = 5^3x-2

Solution

Take ln of both sides

ln 2^2x-1 = ln 5^3x-2

(2x + 1) ln 2 = (3x - 2) ln 5 Using the power to product rule of logs

2x ln 2 + ln2 = 3x ln 5 - 2 ln 5 Multiplying out

2x ln 2 - 3x ln 5 = -ln 2 - 2 ln 5 Separating x terms to the left and others to the right

x(2 ln 2 - 3 ln 5) = -ln 2 - 2 ln 5 Factoring out the x

                  -ln 2 - 2 ln 5
        x =                                  = 1.1365    Dividing by 2 ln 2 - 3 ln 5
                   2 ln 2 - 3 ln 5

C. (10 Points) Use a calculator to evaluate log₇ 51

Solution

First use the change of base formula

                            log 51
        log₇ 51 =
                            log 7

Now put this in your calculator to get

2.02055867514

Problem 2

The clarity C (in feet) of Lake Tahoe t years since 1990 can be modeled by the equation

C(t) = 45e^-t/25

A. (9 Points) How clear was the lake in 1995.

Solution

The year 1995 corresponds to t = 5. Plug this in for t to get

C(5) = 45e^-5/25 = 36.84

The clarity of the lake was 36.84 feet in 1995

B. (10 Points) When will the clarity of the lake only be 5 feet?

Solution

Now plug in 5 for C to get

5 = 45e^-t/25

1/9 = e^-t/25 Dividing both sides by 45

ln(1/9) = ln(e^-t/25) Taking the ln of both sides

ln(1/9) = -t/25 Cancelling the ln and the e

-25 ln(1/9) = t Multiplying both sides by -25

t = 54.93

Now turn this back into a date by adding it to 1990

1990 + 54.93 = 2044.93

We can say that towards the end of the year 2044 the clarity of the lake will be only 5 feet.

Problem 3 Sketch the graphs of the given functions:

A. (10 Points) x² + 4y² = 1
9

Solution

First notice that this is an ellipse since both coefficients are positive. Putting the 4 in the denominator gives

x² y² + = 1
9 1/4

So that

a = 3 b = 1/4

The vertices of the ellipse are at

(3,0), (-3,0), (0,1/4) (0,-1/4)

Now plot the points and sketch the ellipse.

B. (10 Points) x² + y² + 2x - 4y - 4 = 0

Solution

First complete the two squares

x² + 2x + (1 - 1) + y² - 4y + (4 - 4) - 4 = 0 Reordering and adding and subtracting b/2 to both

(x + 1)² + (y - 2)² = 9 Factoring, adding -1 - 4 - 4 = -9, and adding 9 to both sides

We recognize this as a circle with center (-1,2) and radius 3. The graph is given below

C. (10 Points)
Solution

This is a square root function, but instead of starting at (0,0), it starts at (4,-1) since plugging in 4 makes the inside of the square root negative and 0 - 1 = -1 gives the y value. We graph below.

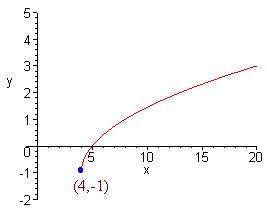
Problem 4 (10 Points) Find the equation of conic with the graph shown below:

Solution

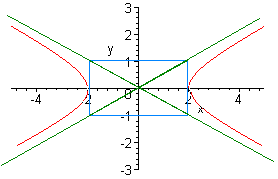
Since this is a hyperbola centered at the origin, we need to determine a, b, and the signs. Since the hyperbola has x intercepts, the coefficient in front of x is positive. We have

a = 2, b = 1

The equation is

x² y² - = 1
4 1

x² - 4y² = 4

Problem 5 (20 Points) Determine whether the function is 1-1. If it is find the inverse and graph both functions on the same set of axes.

A. f(x) = (1/2)^x

Solution

This function is 1-1 since exponentials are 1-1 (they pass the horizontal line test). The inverse of an exponential is a logarithm, that is

f^-1(x) = ln_1/2(x)

Below are the graphs. The red graph is f(x) and the green graph is f^-1(x).

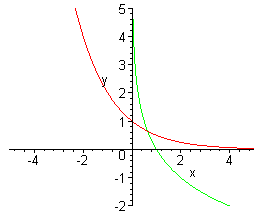
B. f(x) = |x - 4|

Solution

This is not 1-1 since it is a "V" shaped absolute value function. In particular

f(1) = f(5)

Problem 6 Expand each logarithm. Simplify where possible. Assume all variables are such that all expressions are defined.

A. (10 Points) x⁵y² log₃
81

Solution

Use the quotient to difference property of logarithms first:

log₃(x⁵y²) - log₃(81)

= log₃(x⁵) + log₃(y²) - log₃(3⁴) We used the product to sum property.

= 5 log₃(x) + 2 log₃(y) - 4 We used the product to sum property and cancelled the log₃ and 3

B. (10 Points)

Solution

Use the product to sum property of logarithms first and change the root into an exponent.

Warning: Do not cancel the root with the squares, since the "+" is in the way.

log₅(x) + log₅[(y² + 25)^1/2]

= log₅(x) + 1/2 log₅(y² + 25)

Problem 7 Answer the following True or False. If True, explain your reasoning, if False, explain your reasoning or show a counter-example.

A. (7 Points) The domain of the function y = log_b x is (0, ) for all b > 0.

Solution

True, the domain of the log is the range of the exponential which takes on all positive numbers

B. (7 Points) The equation is undefined since you cannot take the square root of a negative number.

Solution

False, this equation is defined for all x less than or equal to zero.

C. (7 Points) If f(x) = x³ + x then f ^-1(3) = 1.

Solution

False, since

f(1) = 1³ + 1 = 2 3

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

Questions, Comments and Suggestions: Email: greenl@ltcc.edu