Practice Exam 1

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Problem 1 

Solve the inequality.  Write the solution on a number line.

        2x² - 5x  >  3

Solution

We first bring all terms to the left hand side and factor

         2x² - 5x - 3  >  0

           (2x + 1)(x - 3)  >  0

The key points occur when the left hand side equals 0 that is

        x   =   -1/2    or    x  =  3

Cut the number line into the regions 

1. to the left of -1/2
   

2. between -1/2 and 3
   

3. to the right of 3

Now set up the table

Since the inequality is ">" we want the positive regions.  We include the endpoints -1/2 and 3.  Our solution is 

        (-, -1/2]  U  [3, )

Problem 2 

Solve  x^1/2 + 2x^1/4 - 8  =  0 

Solution

Let    

        u  =  x^1/4         u²  =  x^1/2  

Substituting gives

        u² + 2u - 8  =  0

        (u - 2)(u + 4)  =  0

        u  =  2    or    u  =  -4

Resubstituting gives

        2  =   x^1/4     or    -4  =  x^1/4 

        (2)⁴  =  (x^1/4)⁴    or    (-4)⁴  =  (x^1/4)⁴ 

        x  =  16    or    x  =  256

Now we verify that 16 is a solution, however plugging 256 back in doe not yield 0.  Hence the only solution is x  =  16.

Problem 3 

Solve

  Solution

First isolate the square root sign

Now square both sides

        x - 3  =  (3 - x)²  =  x² - 6x + 9

        x² - 7x + 12  =  0        bringing to the right and combining like terms

        (x - 3)(x - 4)  =  0        factoring

        x  =  3        or        x  =  4

Notice that plugging in 3 works while plugging in 4 does not work.  The solution is x  =  3.

Problem 4  The graph of y = x² + 2 is shown below.  Find the equation of the other parabola.

Solution

The other graph is the same as the original graph but shifted to the right by 3 units.  Hence the equation is

        y  =  (x - 3)² + 2

Problem 5

Find the domain and range of 

        y  =  x² + 5

Solution

This is a concave up parabola with vertex at (0,5).  Since any number is a valid input of this function, the domain is (-,).  The range begins at 5 and then continues indefinitely, that is, the range is [5,).

Problem 6

Find the domain of

            x² - 5x - 1
                                                    
          x³ - 3x² + 2x

  Solution

        The domain of a rational function is the set of all x such that the denominator is nonzero.

             x³ - 3x² + 2x   =  0

            x(x² - 3x + 2)  =  0

            x(x - 2)(x - 1)  =  0

            x  =  0,    x  =  2,    or   x  =  1

so the domain is 

        {x| x  0, x  2, x 1}

Problem 7

Answer the following True or False.  If True, explain your reasoning, if False, explain your reasoning or show a counter-example.

A.     (7 Points)  All parabolas y = ax² + bx + c are graphs of functions.

Solution

        True, since these parabolas pass the vertical line test.

B.     (7 Points)  If the vertex of the parabola y = ax² + bx + c  has positive y-coordinate and the parabola is concave up, then the parabola has two x-intercepts.

Solution

False,  it will have no x-intercepts.  For example, y  =  x² + 1 has no x-intercepts.

C.     (7 Points)  If a graph has two y-intercepts then the graph is not the graph of a function.

  Solution

True, is it has two y-intercepts then there are two y values that come from the same x value.

Problem 8

If 

        f(x)  =  x² - x        and         g(x) = 2x + 1

find

A.  gog ^-1(x)

Solution

This is always x, since the function of its inverse is always x.

B.  f^.g(2)

We have

        f(2)  =  2² - 2  =  2

and

        g(2)  =  2(2) + 1  =  5

so that

        f^.g(2)  =  (2)(5)  =  10

B.  gof(3)

We have

        f(3)  =  3² - 3  =  6

and

        gof(3)  =  g(6)  =  2(6) + 1  =  13

C.  fof(x)

        fof(x)  =  f(x² - x)  =  (x² - x)² - (x² - x)

        =  x⁴ - 2x³ + x² - x² + x

        =  x⁴ - 2x³ + x

Problem 9

Use the graphs to find gof(1)

Solution

The graph shows us that

        f(1)  =  3

so that

        gof(1)  =  g(3)

The graph of g goes through the x-axis at this point hence

        g(3)  =  0

Problem 10

The graph of f(x) is shown below.  Sketch the graph of f ^-1(x).

Solution

The inverse graph is just the original graph reflected about the line y = x. 

Problem 11

If the graph of f(x) = b^x passes through (2,16), find f(3).

Solution

We have

        16  =  b²

so that

        b  =  4

Hence

        f(3)  =  4³  =  64

Problem 12

Graph the quadratic function.  Label any intercepts, the vertex, and the axis of symmetry.

        y  =  -2x² + 4x + 6

Solution

The x-coordinate of the vertex is 

         x  =  -b/2a  =  -4/-4  =  1

Now plug 1 into the equation to get

        y  =  -2(1)² + 4(1) + 6  =  8

Hence the vertex is at (1,8).

To find the y-intercept plug in 0 for x to get

        (0,6)

To find the x-intercept, plug in 0 for y to get

        0  =  -2x² + 4x + 6

        0  =  x² - 2x - 3        Dividing by -2

        0  =  (x - 3)(x + 1)    Factoring

        x  =  3  or   x  =  -1    The zero product rule

The x-intercepts are 

        (3,0)    and    (-1,0)

Notice that the coefficient of x² is negative, so the graph is concave down. Now plot the points and sketch the graph.

Problem 13

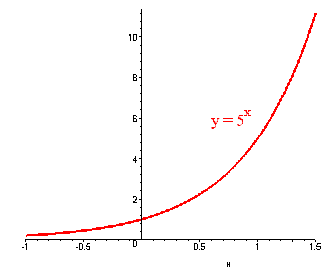
Sketch the graph of y = 5^x.

Solution

This is an exponential function. We first find a few points.

The graph is shown below

Problem 14

Solve for w in 

        2^2w  =  1/256

Solution

We turn this into a log equation to get

        2w  =  log₂(1/256)  =  -log 256

This log is 8 (powers of 2 are 2, 4, 8, 16, 32, 64, 128, 256) hence

        2w  =  -8

or

        w  =  -4

Problem 15

When a certain radioactive element decays, the amount to the element A at any time t is given by

        A  =  25 (2^t/1500)

How much of the element will be left after 3000 years?

Solution

We plug 3000 into this equation for t to get

        A  =  25 (2^3000/1500)  =  (25)2²  =  100

Problem 16

One muffin, two pies, and three cakes cost $23.  One Muffin, three pies , and two cakes cost $21.  One muffin, four pies, and five cakes cost $39.  Find the cost of each.

Let

        x  =  the cost per muffin

        y  =  the cost per pie

        z  =  the cost per cake

We get three equations:

        x + 2y + 3z  =  23

        x + 3y + 2z  =  21

        x + 4y + 5z  =  39

Subtracting the second equation from the first gives

        -y + z  =  2

Subtracting the second equation from the third gives

        y + 3z  =  18

Now add the two equations above to get

        4z  =  20

        z  =  5    dividing by 4

Plugging z  =  5 back into the equation above to get

        y + 3(5)  =  18

        y  =  3        subtracting by 15

Now plug in y  =  3 and z  =  5 into the first original equation to get

        x + 2(3) + 3(5)  =  23

        x + 21  =  23            6 + 15  =  23

        x  =  2                       Subtracting 2 from both sides

Now plug in (2,3,5) into the second and third equations to check.

        2 + 3(3) + 2(5)  =  21

        2 + 4(3) + 5(5)  =  39

We can conclude that the muffins cost $2, the pies cost $3, and the cake costs $5.