Please work out each of the given
problems. Credit will be based on
the steps that you show towards the final answer.
Show your work.
log7 x = y
Solution
7y = x
Problem 2 Find the value of
Solution
y = log9 27
y = 3/2
We can conclude that
y = log9 27
Problem 3 Find the domain of
x2 - 5x - 1
x3 - 3x2 + 2x
Solution
The domain of a rational function is the set of all x such that the denominator is nonzero.
x3 - 3x2
+ 2x
x(x2 - 3x + 2) = 0
x(x - 2)(x - 1) = 0
x = 0, x = 2, or x = 1
so the domain is
{x| x ![]() 0,
x
0,
x ![]() 2,
x
2,
x ![]() 1}
1}
A. All parabolas y = ax2 + bx + c are graphs of functions.
Solution
True, since these parabolas pass the vertical line test.
B. If the vertex of the parabola y = ax2 + bx + c has positive y-coordinate and the parabola is concave up, then the parabola has two x-intercepts.
Solution
False, it will have no x-intercepts. For example, y = x2 + 1 has not x intercepts.
C. If a graph of a function has two x-intercepts then the function is not 1-1.
Solution
True, is it has two x-intercepts then there are two x values that come from the same y value. Also, the x-axis is a horizontal line that will pass through the graph at twice, violating the horizontal line test.
Let f(x) = 3x + 2, g(x) = x + 3, and c(x) = -1. Find
A) f ° g (x)
Solution
f(g(x)) = f(x + 3) = 3(x+ 3) + 2 = 3x + 11
B) f(x + h) - f(x)
h
Solution
f(x + h) = 3(x + h) + 2
so
f(x + h) - f(x) = 3(x + h) + 2 - (3x + 2) = 3x + 3h + 2 - 3x - 2 = 3h
Dividing by h gives
f(x + h) - f(x)
3h
=
=
3
h
h
C) g(f(1))
Solution
f(1) = 3(1) + 2 = 5
g(f(1)) = g(5) = 5 + 3 = 8
D) c ° f (2)
Solution
f(2) = 3(2) + 2 = 8
c(8) = -1 c is always -1
E)
c(x)g(x)
f(x) - 7c(x)
Solution
3x + 2 - 7(-1) 3x + 9 3(x + 3) 3
Problem 6 You are constructing a rectangular room such that one side of the room is 14 feet longer than the other side, and the distance from opposite corners is 26 feet. What are the dimensions of the room? Give your answer accurate to two decimal places.

We use the Pythagorean Theorem
x2 + (x + 14)2 = 262
x2 + x2 + 28x + 196 = 676 Multiplying out
2x2 + 28x - 480 = 0 combing like terms and bringing to the left
x2 + 14x - 240 = 0 Dividing by 2
(x + 24)(x - 10) = 0 factoring
x = 10 x cannot be negative
The dimensions are 10 x 24.
Problem 7 Graph the quadratic function. Label any intercepts, the vertex, and the axis of symmetry.
y = -2x2 + 4x + 6
Solution
The x-coordinate of the vertex is
x = -b/2a = -4/-4 = 1
Now plug 1 into the equation to get
y = -2(1)2 + 4(1) + 6 = 8
Hence the vertex is at (1,8).
To find the y-intercept plug in 0 for x to get
(0,6)
To find the x-intercept, plug in 0 for y to get
0 = -2x2 + 4x + 6
0 = x2 - 2x - 3 Dividing by -2
0 = (x - 3)(x + 1) Factoring
x = 3 or x = -1 The zero product rule
The x-intercepts are
(3,0) and (-1,0)
Notice that the coefficient of x2 is negative, so the graph is concave down. Now plot the points and sketch the graph.

Problem 8 The
graphs of y = f(x) and y =
g(x) are given below. Find
A.
f(0)

B. g(-1)
C. g ° f (1)
D. f(1)
g(-1)
A. f(0) is the y-intercept of the graph of f(x) which is -1.
B. g(-1) = 1 since the graph goes through (-1,1).
C. Since f(1) = -1, we plug -1 into g. g(-1) = 1.
D. f(1) = -1, g(-1) = 1. Now divide to get -1/1 = -1.
Problem 9 Find the domain and range of the following functions
A. f(x) = 2x-1 + 3
Solution
This function is an exponential function. Exponential functions have all real numbers as their domain. The range of the "unshifted" exponential function is all real numbers greater than 0. Since this function is shifted up by 3, the new range will also shift up by 3. Thus the range is all real numbers greater than 3. Notice that the horizontal shift "right 1" does not affect the domain or the range.
B. f(x) = log8(x+2) - 4
Solution
This function is a logarithm function. The "unshifted logarithm functions have all numbers greater than 0 as its domain. Since this function is shifted 2 to the left, the domain is also shifted 2 to the left. Thus the domain is all real numbers greater than -2. The range of logarithm function is all real numbers. Notice that the vertical shift "down 4" does not affect the range.
Problem 10
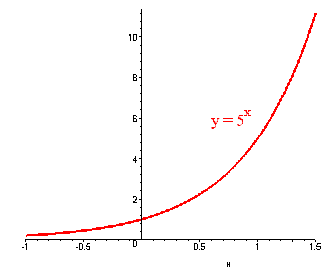
Sketch the graph of y = 5x.
Solution
This is an exponential function. We first find a few points.
| x | 0 | 1 | -1 |
| y | 1 | 5 | 1/5 |
The graph is shown below
Problem 11
Solve for w in
22w = 1/256
Solution
First notice that 256 is a power of 2 (powers of 2 are 2, 4, 8, 16, 32, 64, 128, 256) hence
1/256 = 28
256 = 2-8
We have
22w = 2-8
so that
2w = -8
or
w = -4
Problem 12
When a certain radioactive element decays, the amount to the element A at any time t is given by
A = 25 (2t/1500)
How much of the element will be left after 3000 years?
Solution
We plug 3000 into this equation for t to get
A = 25 (23000/1500) = (25)22 = 100
Problem 13
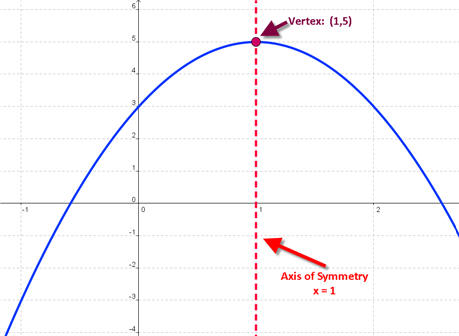
Sketch the graph of the function below. Label the vertex and the axis of symmetry.
y = -2(x - 1)2 + 5
Solution
This is a parabola in standard form. The "-2" causes the parabola to be steeper and to be concave down since the coefficient is negative. The "- 1" shifts the parabola to the right 1. The "+ 5" shifts the parabola up 5. Thus the vertex is (1,5) and the axis of symmetry is x = 1.
The graph is shown below.
Problem 14
If
f(x) = log3(2x - 1)
find
f -1(x)
Solution
First set
y = log3(2x - 1)
And switch the x and y.
x = log3(2y - 1)
Next, since the log is the inverse of the exponential, we can put this into exponential form.
3x = 2y - 1
Now add 1 to both sides to get
3x + 1 = 2y
Finally, divide both sides by 2 to get
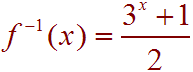
Problem 15
The graph if the function y = f (x) is shown below. Determine if this function is 1-1.

Solution
Since every horizontal line passes through this graph at most once, it passes the horizontal line test. Thus the function is 1-1.