MATH 154 Practice Exam 2  Key

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

 

Problem 1   Write as an exponential function

        log7 x  =  y  

Solution
The base of the log is 7, so the base of the exponent will also be 7.  The log and the exponential are inverses of each other, so the x and the y switch.  We get

7y  =  x



Problem 2 Find the value of
log9 27

Solution
We first turn

y  =  log9 27

into exponential form.  We get
9y  =  27
Notice that 9 and 27 are both powers of 3:
32y  =  33
We can set the exponents equal to each other to get
2y  =  3

y  =  3/2

We can conclude that

y  =  log9 27


Problem 3   Find the domain of 

           x2 - 5x - 1
                                                    
          x3 - 3x2 + 2x

Solution

        The domain of a rational function is the set of all x such that the denominator is nonzero.

             x3 - 3x2 + 2x   =  0

            x(x2 - 3x + 2)  =  0

            x(x - 2)(x - 1)  =  0

            x  =  0,    x  =  2,    or   x  =  1

so the domain is

        {x| x  0, x  2, x 1}

Problem 4

Answer the following True or False.  If True, explain your reasoning, if False, explain your reasoning or show a counter-example.

A.     The exponential function y = bx has y-intercept 1 and the logarithmic function y = logbx has x-intercept 1 for any b >0 with b not equal to 1.
Solution
True, the exponential goes through the point (0,1) since b0 = 1 for any such b.  The log is the inverse and the x-intercept of the inverse is the y-intercept of the original function.

B.     If a graph of a function has two x-intercepts then the function is not 1-1.

Solution

True, is it has two x-intercepts then there are two x values that come from the same y value.  Also, the x-axis is a horizontal line that will pass through the graph at twice, violating the horizontal line test.  


Problem 5 

Let f(x) = 3x + 2, g(x) = x + 3, and c(x) = -1.  Find

 

A)     f ° g (x)  

Solution

        f(g(x))  =  f(x + 3)  =  3(x+ 3) + 2  =  3x + 11

B)        f(x + h) - f(x)
                                                  
                    h

Solution

        f(x + h)  =  3(x + h) + 2

so

        f(x + h) - f(x)  =  3(x + h) + 2 - (3x + 2)  =  3x + 3h + 2 - 3x - 2  =  3h

Dividing by h gives

         f(x + h) - f(x)              3h
                                    =              =  3
                  h                         h

C)   g(f(1))     

Solution

        f(1)  =  3(1) + 2  =  5

        g(f(1))  =  g(5)  =  5 + 3  =  8

D)   c ° f (2)     

Solution

        f(2)  =  3(2) + 2  =  8

        c(8)  =  -1    c is always -1

E)         c(x)g(x)
                                               
            f(x) - 7c(x)

Solution

  Plugging in, we get

             (-1)(x + 3)                -x - 3            -(x + 3)                 1
                                       =                   =                        =  -             
            3x + 2 - 7(-1)            3x + 9            3(x + 3)                3

 

Problem 6  The graphs of y = f(x) and y = g(x) are given below.  Find

A.      f(0)

B.    g(-1)

C.     g ° f (1)  

D.         f(1)
                             
    g(-1)

 

  Solutions

A.  f(0) is the y-intercept of the graph of f(x) which is -1.

B.  g(-1)  =  1 since the graph goes through (-1,1).

C.  Since f(1)  =  -1, we plug -1 into g.  g(-1)  =  1.

D.  f(1)  =  -1, g(-1)  =  1.  Now divide to get -1/1  =  -1.

 

Problem 7  Find the domain and range of the following functions

A.  f(x)  =  2x-1 + 3

Solution

This function is an exponential function.  Exponential functions have all real numbers as their domain.  The range of the "unshifted" exponential function is all real numbers greater than 0.  Since this function is shifted up by 3, the new range will also shift up by 3.  Thus the range is all real numbers greater than 3.  Notice that the horizontal shift "right 1" does not affect the domain or the range.

B.  f(x)  =  log8(x+2) - 4

Solution

This function is a logarithm function.  The "unshifted logarithm functions have all numbers greater than 0 as its domain.  Since this function is shifted 2 to the left, the domain is also shifted 2 to the left.  Thus the domain is all real numbers greater than -2.  The range of logarithm function is all real numbers.  Notice that the vertical shift "down 4" does not affect the range.

Problem 8

Sketch the graph of y = 5x.

Solution

This is an exponential function. We first find a few points.

x 0 1 -1
y 1 5 1/5

The graph is shown below

       

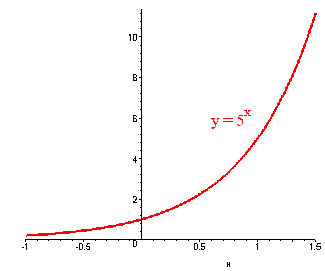
Problem 9

Solve for w in 

        22w  =  1/256

Solution

First notice that 256 is a power of 2 (powers of 2 are 2, 4, 8, 16, 32, 64, 128, 256) hence

1/256  =  28

256  =  2-8

We have

22w  =  2-8

so that

2w  =  -8

or

        w  =  -4

 

Problem 10

When a certain radioactive element decays, the amount to the element A at any time t is given by

        A  =  25 (2t/1500)

How much of the element will be left after 3000 years?

Solution

We plug 3000 into this equation for t to get

        A  =  25 (23000/1500)  =  (25)22  =  100

 

 

Problem 11

If

f(x)  =  log3(2x - 1)

find

f -1(x)

Solution

First set

y  =  log3(2x - 1)

And switch the x and y.

x  =  log3(2y - 1)

Next, since the log is the inverse of the exponential, we can put this into exponential form.

3x  =  2y - 1

Now add 1 to both sides to get

3x + 1  =  2y

Finally, divide both sides by 2 to get

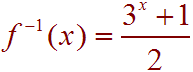
f^-1 (x) = (3^x + 1) / 2

Problem 12

The graph if the function y = f (x) is shown below.  Determine if this function is 1-1.

Graph of a function that rises up and to the right continuously

Solution 

Since every horizontal line passes through this graph at most once, it passes the horizontal line test.  Thus the function is 1-1.