Practice Exam 1

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Back to the Practice Exam

Problem 1  Solve the inequality.  Write the solution on a number line.

2x2 - 5x > 3

Solution

First subtract 3 from both sides to set the inequality to 0.

2x2 - 5x - 3 > 0

Then factor.  This can be done in many ways.  It is assumed that intermediate algebra students know how to factor.

(2x + 1)(x - 3) > 0

Now find the zeros by setting each factor equal to 0. 

2x + 1 = 0     x - 3 = 0

x = -1/2       x = 3

Notice that this splits the interval into three regions.  Use a test point to check each region.

Test Point 2x + 1 x - 3 Total Sign Included in Solution ( > 0)
-1 -1 -4 + Yes
0 1 -3 - No
4 9 1 + Yes

We can conclude that the solution is

(-infinity,-1/2) U (3,infinity)

 

Problem 2  Solve the inequality.  Write the solution on a number line.

(4x-3)/(x+5) <= 0 

The key points here are

x = -5   and   x = 3/4

Since these two values also split the number line into three regions, we use the test point method again.

Test Point 4x - 3 x + 5 Total Sign Included in Solution ( < 0)
-6 -27 -1 + No
0 -3 5 - Yes
1 1 6 + No

Since the "-5" comes from the denominator, that endpoint is not included no matter what the inequality.  Thus the solution is

(-5,3/4]

 

Problem 3  Solve

x1/2 - 2x1/4 - 8  =  0

Solution

Use substitution with

u = x1/4

Then

u2 = x1/2

The substitution gives

u2 - 2u - 8  =  0

Factor to get

(u - 4)(u + 2) = 0

u = 4     or     u = -2

Next resubstitute to get

x1/4 = 4     or     x1/4 = -2

Next take 4th powers to get

x = 44 = 256     or     x = (-2)4 = 16

Plugging 256 and 16 into the original equation gives

16  - 8 - 8 = 0

4 - 4 - 8 = -8

Since the first is zero and the second is not zero, only the first solution is valid.  Thus the solution is

x = 256

Problem 4  Solve

root(x-3) + x = 3 

Solution

Subtract x from both sides to get

(root(x-3))^2 = (3-x)^2

Cancel the root and the square on the left hand side and FOIL out the right hand side to get

x - 3  =  x2 - 6x + 9

Subtract x - 3 from both sides and then switch left to right to get
x2 - 7x + 12  =  0

(x - 3)(x - 4)  =  0

x  =  3     or     x = 4

Plugging in x = 3 given
0 + 3  =  3

which works.  Now plug in x = 4.
1 + 4 = 5

which does not work.  Therefore the only solution is
x = 3




Problem 5 The graph of y = x2 + 2 is shown below.  Find the equation of the other parabola.

Solution

The parabola on the right is the same as the parabola on the left except it is shifted over to the right 3 units.  Shifting to the right corresponds to subtracting inside of the square.  Thus the equation is

(x - 3)2 + 2

Problem 6  Find the domain of

f(x) = (x^2 - 5x - 1) / (x^3 - 3x^2 + 2x)

Solution

The domain of a function is the set of all x values that can be plugged in.  The only possible issue is that the denominator could be 0, since division by 0 is not allowed in math.  We set

x3 - 3x2 + 2x  =  0

Now factor out the x to get

x(x2 - 3x + 2)  =  0

x(x - 1)(x - 2)  =  0

x = 0     or     x = 1     or     x = 2

 

Problem 7  Solve the following system of equations

3x - 2y  + 4z = 1
2x +  y -  5z  = 3
4x - 5y + 13z = -1

Solution

First take the first equation and add twice the second equation to eliminate the y.

3x  - 2y  + 4z = 1
4x + 2y - 10z = 6
7x         - 6z = 7   (*)

Next add five time the second equation to the third equation to eliminate the y.

10x + 5y -  25z  = 15
  4x - 5y + 13z = -1
14x        - 12z  =  14     (**)

Multiply (*) by -2 and add it to (**) to get

14x - 12z  =  14
14x - 12z  =  14
      0       =  0

Thus there is no solution

 

Problem 8  One muffin, two pies, and three cakes costs $23.  One muffin, three pies, and two cakes cost $21.  One muffin, four pies and five cakes costs $39.  Find the cost of each.

Solution

Let

        x  =  the cost per muffin

        y  =  the cost per pie

        z  =  the cost per cake

We get three equations:

        x + 2y + 3z  =  23

        x + 3y + 2z  =  21

        x + 4y + 5z  =  39

Subtracting the second equation from the first gives

        -y + z  =  2

Subtracting the second equation from the third gives

        y + 3z  =  18

Now add the two equations above to get

        4z  =  20

        z  =  5    dividing by 4

Plugging z  =  5 back into the equation above to get

        y + 3(5)  =  18

        y  =  3        subtracting by 15

Now plug in y  =  3 and z  =  5 into the first original equation to get

        x + 2(3) + 3(5)  =  23

        x + 21  =  23            6 + 15  =  23

        x  =  2                       Subtracting 2 from both sides

Now plug in (2,3,5) into the second and third equations to check.

        2 + 3(3) + 2(5)  =  21

        2 + 4(3) + 5(5)  =  39

We can conclude that the muffins cost $2, the pies cost $3, and the cake costs $5.

 

Problem 10  Graph the piecewise defined function.  Then use the graph to determine the domain and range of the function.

f(x) = {x+1 if x < 2, 5-2x if x >=2

First notice that both pieces are pieces of lines.  The first is a line with y-intercept 1 and slope 1.  This piece should stop at x = 2.  Plugging in, gives y = 3.  Thus we plot an open circle at the point (2,3) since the inequality does not have an equals sign.  For the second piece, plus in x = 2 to get y = 1.  Thus the line starts with a closed circle at the point (2,1) since the inequality does have an equals sign.  The slope is -2 so rise down 2 and run right 1.

The graph is shown below.

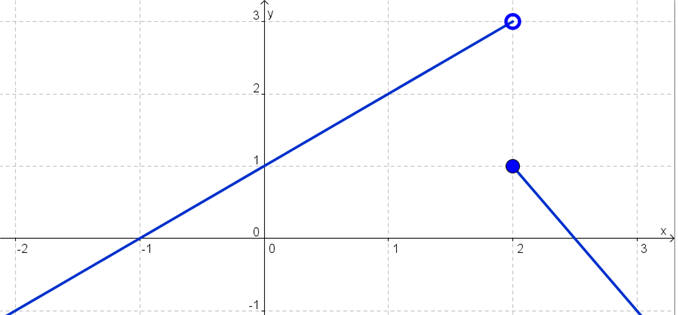
Piecewise graph with left ray through (1,0) and (2,3) right at (2,1) and (3,-1)

 

The domain is all real numbers (negative infinity, infinity) since any value of x can be plugged in.  Notice that there is no lower bound to the graph, but the graph only gets as high as y = 3 and not including this value.  Therefore the range is (negative infinity, 3).

 

Problem 11  Consider the graph of y = f(x) shown below.

Graph of y = f(x) through (-1,1), (0,1), (1,-1), (2,1)

A.  Find f(2)

Solution

This is the point on the graph when x = 2.  Since the graph goes through the point (2,1), f(2) = 1.

B.  Find all values of x such that f(x) = 1.

Solution

We look for all points on the graph that have y coordinate 1.  These points are (-1,1), (0,1), and (2,1).  Thus the values of x with f(x) = 1 are x = -1, x = 0, and x = 2.

 

Problem 12  Answer the following true or false.  If true, explain your reasoning.  If false, explain your reasoning or provide a counter example.

A.  If a graph has two y-intercepts, the graph is not the graph of a function of y in terms of x.

Solution

True, since the y-axis is a vertical line, this line crosses the graph twice violating the vertical line test.

B.  If (1,5) and (2,5) are two ordered pairs of a relation, then the relation cannot be a function.

Solution

False, it is ok for a function to have repeated y values.  It is not ok to have repeated x values when the y values are different.

C.  The graph of y = f(x+1) + 2 is the same as the graph of y = f(x) but shifted one to the right and two upwards.

Solution

False, it is shifted one to the left and two upwards.  Notice that plugging in x = -1 makes the inside of the function 0, thus one to the left.