Exercises Involving Distance and Circles
1. The distance between points (a,b) and (c,d)
is
![]() .
.
3. The circle with radius r and center at the point (0,k) is given by the equation x2 + (y - k)2 = r2.
5. If the distance between the point P and the point (3,4) is 5, then P must be the origin.
False, P could be any point on the circle with radius 5 and center (3,4).
7. P = (0,0) and Q = (4,3)
The distance is 5.
9. P = (1,-3) and Q = (7,-11)
The distance is 10.
11. P = (a,4) and Q = (a + 2, 3)
The distance is ![]()
13. P = (a,b) and Q = (b,a)
The distance is
![]()
15. P = (1,2) and Q is the intersection of the lines 2x + y = 7 and 5x - 2y = 4.
The distance is ![]()
17. P = (-2,1) and Q is the y-intersect of the line 3x + 2y = 1.
The distance is
![]()
19. Center (0,0) and radius 5.
x2 + y2 = 25
21. Center (2,-4) and radius 3.
(x - 2)2 + (y + 4)2 = 9
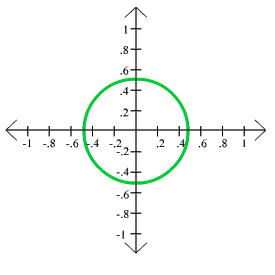
23. 4x2 + 4y2 = 1
Center: (0,0) Radius: 1/2
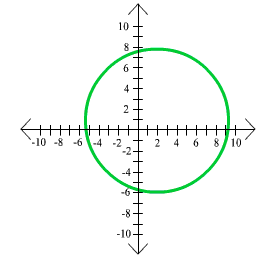
25. (x - 2)2 + (y + 1)2 = 49
Center: (2,-1) Radius: 7
27. (x + 2)2 + (y - 2)2 = 4
Center: (-2,2) Radius: 2

29. (x + 2)2 + (y + 1)2 = 2
Center: (-2,-1) Radius: ![]()

31. x2 + y2 + 6x = 7
Center: (-3,0) Radius: 4
33. x2 + y2 = 2x + 8
Center: (1,0) Radius: 3
For exercise 33 through 36 find equation of the circle with the given information. Then sketch the graph.
35. The circle with center (3, -2) that contains the point (6, 2).
(x - 3)2 + (y + 2)2 = 25
37. The circle with radius 3 that contains the points (-1, 2) and (-1, 8).
(x + 1)2 + (y - 5)2 = 9
For exercises 37 through 40, find the equation of the circle.
39. 
x2 + y2 = 9
41. 
(x - 3)2 + (y - 2)2 = 4
43.
(x - 3)2 + (y + 3)2 = 1

45. Center at (0,0) and passes through the point (0,4).
x2 + y2 = 16

47. Center at (0,0) and passes through the point (2,4).
x2 + y2 = 20

49. Center at (3,1) and passes through the point (4,5).
(x - 3)2 + (y - 1)2 = 17
