Name                          .

 

Math 152B Final

Please do all of the following problems.  All work and all answers must be done on your own paper.  Credit earned will be based on the steps that you show that lead to the final solution.  Good Luck!

 

 

Problem 1:  Factor the following

A)      x5y2 - x3y4   

Solution:  

        x5y2 - x3y4   =   x3y2(x2 - y2)    Pulling out the GCD

        =  x3y2(x - y)(x + y)    Difference of Squares

 

B)     6x2 + 5x - 6   

Solution:

        AC  =  6(-6)  =  -36        We use the AC method

        (-4,9)        Finding two numbers that add to -36 and multiply to 5

        6x2 + 5x - 6  =  6x2 - 4x + 9x - 6     Using 5x  =  -4x + 9x

        =  2x(3x - 2) + 3(3x - 2)        Factoring by grouping     

        =  (3x - 2)(2x + 3)        Pulling out the GCD of 3x - 2

C)     x3 + x2 - 4x - 4   

  Solution

        x3 + x2 - 4x - 4  =  x2(x + 1) - 4(x + 1)     Factor by grouping

        =  (x + 1)(x2 - 4)         Pulling out the GCD

        =  (x + 1)(x - 2)(x + 2)    Difference of Squares

 

Problem 2:   Perform the indicated operations and simplify

A)       x3 + 3x2 + 2x
                                   ÷  (x2 + 2x)
               x - 1                                         

 

Solution

            x(x2 + 3x + 2)
                                   ÷  x (x + 2)        Pulling out the GCD's
               x - 1                                         

 

                    x(x + 2)(x + 1)              x (x + 2)
          =                                    ÷                                Factoring and writing over 1.
                           x - 1                            1
        

                    x(x + 2)(x + 1)                    1
          =                                    ×                                Multiplying by the reciprocal.
                           x - 1                        x(x + 2)

                     x + 1          1
          =                     ×                  Cross canceling
                     x - 1           1  

                    x + 1       
          =                           Simplifying
                    x - 1        


B)           10                   5
                              -                   
             h - 10              h - 5               

  Solution

               10(h - 5)                   5(h - 10)
      =                               -                               Creating a common denominator
             (h - 10)(h - 5)          (h - 5)(h - 10)    

 

               10(h - 5) - 5(h - 10)     
      =                                                Creating a common denominator
                  ( h - 10)(h - 5)      

 

               10h - 50 - 5h + 50     
      =                                                Multiplying through (remember to multiply the "-" through)
                  ( h - 10)(h - 5)      

 

                      5h     
      =                                      Combining like terms
               (h - 10)(h - 5)      

 

Problem 3: Solve

A)   

Solution

        x + 2  =  x2         Squaring both sides

        x2 - x - 2  =  0      Moving all terms to the right and then switching left and right.

        (x - 2)(x + 1)  =  0        Factoring

        x - 2  =  0    or    x + 1  =  0        The zero product property

        x  =  2    or    x  =  -1        Solving

Notice that x  =  2 works in the original equation, but x  =  -1 does not work, since a root can never produce a negative number.  Hence the solution is x  =  2

 

B)   x3 + 2x2 + x  =  0 

  Solution

        x(x2 + 2x + 1)  =  0        Factor out the GCF

        x(x + 1)2  =  0        Square of a sum

        x  =  0    or    (x + 1)2  =  0        Zero Product Property

        x  =  0    or    x  =  -1        Solving

      

Problem 4:  A motorboat travels 10 mi/hr in still water.  If the boat takes the same amount of time to travel 2 miles upstream as it does to travel 3 miles downstream, find the speed of the current.

  Solution

Let x  =  the speed of the current

We set up a distance rate time table, noting that the rate upstream is the rate in still water minus the speed of the current and the rate downstream is the rate in still water minus plus the speed of the current.

  distance rate time
Up Stream 2 10 - x t
Down Stream 3 10 + x t

 Since 

        d  =  rt

        t  =  d/r

Using the fact that the times are equal gives

               2                 3
                         =                     
          10 - x           10 + x           

  Cross multiplying gives

        2(10 + x)  =  3(10 - x)

        20 + 2x  =  30 - 3x        Multiplying out

        5x  =  10        Adding 3x and subtracting 10 from both sides

        x  =  2        Dividing both sides by 5

The speed of the current is 2 miles per hour.

 

Problem 5:

A) Find the point of intersection of the two lines

        4x - 3y  =  15    and    5x - 6y  =  21  

Solution

        We use the method of elimination:

           8x - 6y  =  30        Multiplying the first equation by 2
           5x - 6y  =  21
     --                               
            3x  =  9                Subtracting the two equations

            x  =  3                    Dividing both sides by 3

        4(3) - 3y  =  15        Substituting x  =  3 into the first equation

        12 - 3y  =  15            Multiplying 

        -3y  =  3                    Subtracting 12 from both sides

    `    y  =  -1                    Dividing by -3

Hence the solution is the point (3,-1)

 

Problem 6: Simplify.  Write your answer without negative exponents.

      

Solution

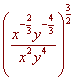
First use the distributive rule, multiplying the 3/2 through each exponent

               x -1 y -2 
        =                  
               x3 y6     

        =  x -1 - 3 y -2 - 6        Using the quotient rule for exponents

        =  x -4 y -8        Subtracting

                 1
        =                         Using the property of negative exponents
              x4 y8       

 

 

Problem 7:  Simplify

A)          

Solution

             FOIL

            Distributing the "-" through

        =  2 -  8        Combining like terms

 

Problem 8:  Solve.  Any complex solutions should be written in the form a + bi.

A)    x2 - 3x -15  =  0  

Solution

The equation does not factor, so we use the quadratic formula:

        a  =  1    b  =  -3    c  =  -15        
        

 

 

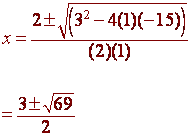
B)   2x2 + 4  =  x   

Solution

        2x2 - x + 4  =  0        Setting everything equal to zero.

The equation does not factor, so we use the quadratic formula:

        a  =  2    b  =  -1    c  =  4

                        

 

C)    3x2 - x - 1  =  0   

Solution

The equation does not factor, so we use the quadratic formula:

        a  =  3    b  =  -1    c  =  -1

       

       

 

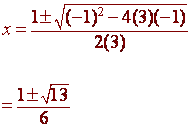
Problem 9  Complete the square

        2x2 - 8x + 3  =  0

Solution

        2(x2 - 4x) + 3  =  0        Factoring out the 2 from the first two terms

        2(x2 - 4x + 4 - 4) + 3  =  0        Adding and subtracting the magic number (4/2)2 

        2[(x - 2)2  - 4] + 3  =  0        Factoring the first three terms 

        2(x - 2)2  - 8 + 3  =  0        Multiplying the 2 through 

        2(x - 2)2  - 5  =  0        Combining like terms 

     

 

Problem 10  Solve the absolute value inequality.

3 - | 2x - 5| < 2

Solution

    First we solve the equality
3 - |2x - 5| = 2
-|2x - 5|  =  -1    Subtract 3 from both sides
|2x - 5|  =  1    Multiply both sides by -1
2x - 5  =  1    or    2x - 5  =  -1    Absolute value equations split up as an "OR" statement
2x  =  6    or    2x  =  4    Add 5 to both sides of the equations
x = 3    or    x = 2    Divide both sides of the equations by 2

Now we find test points to the left of 2, between 2 and 3, and to the right of 3.  We have

3 - |2(0) - 5|  =  3 - |-5|  =  3 - 5  =  -2 < 2

Thus the numbers to the left of 2 are included. 

3 - |2(2.5) - 5|  =  3 - |5 - 5|  =  3 - 0  =  3 > 2

Thus the numbers between 2 and 3 are not included. 

3 - |2(4) - 5|  =  3 - |8 - 5|  =  3 - 3  =  0 < 2

Thus the numbers to the right of 3 are included. 

The final solution is

(-infinity,2)U(3,infinity)

 

Problem 11  Answer the following true or false.  Please explain your reasoning.

  1. If  c  <  0  then 

            x2 + bx + c  =  0
    has two distinct real roots.

    Solution

    Use the discriminant:

            b2 - 4ac  =  b2 - 4c

    Since c < 0, the discriminant is positive, so there are two distinct real roots.  True

     

  2. If x = 2 and x = 4 is a solution of  |ax + b| < c , then x = 3 is also a solution.

            Solution

                True,  Since the inequality is a "<", the solution is between the endpoints.