Name
.
Math 152B Final
Please do all
of the following problems. All work
and all answers must be done on your own paper.
Credit earned will be based on the steps that you show that lead to the
final solution. Good Luck!
Problem
1: Factor the following
A)
x5y2 - x3y4
x5y2 - x3y4 = x3y2(x2 - y2) Pulling out the GCD
= x3y2(x - y)(x + y) Difference of Squares
B)
6x2 + 5x - 6
AC = 6(-6) = -36 We use the AC method
(-4,9) Finding two numbers that add to -36 and multiply to 5
6x2 + 5x - 6 = 6x2 - 4x + 9x - 6 Using 5x = -4x + 9x
= 2x(3x - 2) + 3(3x - 2) Factoring by grouping
= (3x - 2)(2x + 3) Pulling out the GCD of 3x - 2
C)
x3
x3
= (x + 1)(x2 - 4) Pulling out the GCD
= (x + 1)(x - 2)(x + 2) Difference of Squares
Problem
2: Perform the indicated operations and simplify
A)
x3 + 3x2 + 2x
÷ (x2 + 2x)
x -
1
x(x2 + 3x + 2)
÷ x (x + 2) Pulling
out the GCD's
x -
1
x(x + 2)(x +
1)
x (x + 2)
=
÷
Factoring and writing over 1.
x -
1
1
x(x + 2)(x +
1)
1
=
×
Multiplying by the reciprocal.
x -
1
x(x + 2)
x + 1 1
=
×
Cross canceling
x -
1 1
x + 1
=
Simplifying
x -
1
B)
10
5
-
h -
10
h -
5
10(h - 5)
5(h - 10)
=
-
Creating
a common denominator
(h -
10)(h - 5) (h -
5)(h - 10)
10(h - 5) - 5(h - 10)
=
Creating
a common denominator
( h -
10)(h - 5)
10h - 50 - 5h + 50
=
Multiplying
through (remember to multiply the "-" through)
( h -
10)(h - 5)
5h
=
Combining
like terms
(h -
10)(h - 5)
Problem
3: Solve
A)
![]()
x + 2 = x2 Squaring both sides
x2 - x - 2 = 0 Moving all terms to the right and then switching left and right.
(x - 2)(x + 1) = 0 Factoring
x - 2 = 0 or x + 1 = 0 The zero product property
x = 2 or x = -1 Solving
Notice that x = 2 works in the original equation, but x = -1 does not work, since a root can never produce a negative number. Hence the solution is x = 2
B)
x3 + 2x2 + x = 0
x(x2 + 2x + 1) = 0 Factor out the GCF
x(x + 1)2 = 0 Square of a sum
x = 0 or (x + 1)2 = 0 Zero Product Property
x = 0 or x = -1 Solving
Problem
4:
A motorboat travels 10 mi/hr in still water.
If the boat takes the same amount of time to travel 2 miles upstream as
it does to travel 3 miles downstream, find the speed of the current.
Let x = the speed of the current
We set up a distance rate time table, noting that the rate upstream is the rate in still water minus the speed of the current and the rate downstream is the rate in still water minus plus the speed of the current.
| distance | rate | time | |
| Up Stream | 2 | 10 - x | t |
| Down Stream | 3 | 10 + x | t |
Since
d = rt
t = d/r
Using the fact that the times are equal gives
2
3
=
10 -
x 10 +
x
2(10 + x) = 3(10 - x)
20 + 2x = 30 - 3x Multiplying out
5x = 10 Adding 3x and subtracting 10 from both sides
x = 2 Dividing both sides by 5
The speed of the current is 2 miles per hour.
Problem
5:
A) Find the point of intersection of the two lines
4x - 3y = 15
and 5x - 6y = 21
We use the method of elimination:
8x - 6y = 30 Multiplying
the first equation by 2
5x - 6y
= 21
--
3x
=
9
Subtracting the two equations
x = 3 Dividing both sides by 3
4(3) - 3y = 15 Substituting x = 3 into the first equation
12 - 3y = 15 Multiplying
-3y = 3 Subtracting 12 from both sides
` y = -1 Dividing by -3
Hence the solution is the point (3,-1)
Problem
6:
Simplify. Write your answer
without negative exponents.
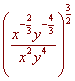
First use the distributive rule, multiplying the 3/2 through each exponent
x -1 y -2
=
x3 y6
= x -1 - 3 y -2 - 6 Using the quotient rule for exponents
= x -4 y -8 Subtracting
1
=
Using the property of negative exponents
x4
y8
Problem
7: Simplify
A)
![]()
![]() FOIL
FOIL
![]() Distributing the "-" through
Distributing the "-" through
= 2![]() - 8 Combining
like terms
- 8 Combining
like terms
Problem
8: Solve. Any
complex solutions should be written in the form a + bi.
A)
x2 - 3x
-15 = 0
The equation does not factor, so we use the quadratic formula:
a = 1 b = -3 c
= -15
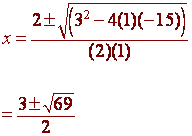
B)
2x2 + 4 = x
2x2 - x + 4 = 0 Setting everything equal to zero.
The equation does not factor, so we use the quadratic formula:
a = 2 b = -1 c = 4

C)
3x2
- x - 1 = 0
The equation does not factor, so we use the quadratic formula:
a = 3 b = -1 c = -1
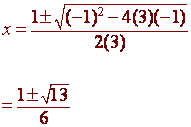
Problem 9 Complete the square
Problem
10 Determine whether there is one real root, two real roots or two complex roots.
Do not find the roots.
A.
2x2 + 16x + 32
The discriminant is
b2 - 4ac = 162 - 4(2)(32)
= 256 - 256 = 0
Since the discriminant is 0 there is exactly one rational root.
B.
2x2 - 5x - 10
The discriminant is
b2 - 4ac = (-5)2 - 4(2)(-10)
= 25 + 80 < 0
Since the discriminant is positive there are two real roots.
C. 12341234234x2 - 3x + 12341324123123523
The discriminant is
b2 - 4ac = (-3)2 - 4(Big)(Bigger)
= 9 - SuperBig < 0
Since the discriminant is negative there are no real roots, only two complex roots.
Problem 11 Answer the following true or false. Please explain your reasoning.
-
If c < 0 then
x2 + bx + c = 0
has two distinct real roots.
Solution
Use the discriminant:
b2 - 4ac = b2 - 4c
Since c < 0, the discriminant is positive, so there are two distinct real roots. True -
If x = 2 and x = 4 is a solution of |ax + b| < c , then x = 3 is also a solution.
True, Since the inequality is a "<", the solution is between the endpoints.