Name                          .

 

Math 152B Practice Exam 3 Key

Please do all of the following problems.  All work and all answers must be done on your own paper.  Credit earned will be based on the steps that you show that lead to the final solution.  Good Luck!

 

Problem 1: 

Write down the quadratic formula

 Solution  

If

        ax2 + bx + c  =  0

then

       

 

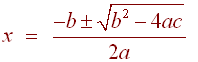
Problem 2:

Find the root: 

         

Solution

        -2, since (-2)3 = -8

 

Problem 3: Simplify the expression.  Leave your answer in exponential form with only positive exponents.

       

 

 Solution

       

 

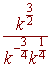
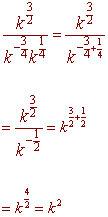
Problem 4:

Use the discriminant to determine the nature of the roots of the following quadratics.

A.     2x2 + 3x + 4  =  0

Solution

The discriminant is

        32 - 4(2)(4) = 9 - 32 < 0

Since the discriminant is negative, we can conclude that there are no real roots, only two complex conjugate roots.

B.    3x2 + x - 4  =  0 

Solution

The discriminant is

        12 - 4(3)(-4) = 1 + 48 > 0

Since the discriminant is positive, we can conclude that there are two distinct real roots.

C.      4354324532453x2 + 2x + 6798797698766  =  0

Solution

The discriminant is two difficult to compute by hand, however we see that the second coefficient is small in comparison to the other two coefficients, that is

        22 - 4(big)(big) = 4 - very big < 0

Since the discriminant is negative, we can conclude that there are no real roots, only two complex conjugate roots.

 

Problem 5:   Multiply and Simplify

       

 

Solution

       

 

Problem 6:  

Solve the equation by using the factoring or root method.

A) 10x2  =  13x + 3 

          

Solution

First bring all terms to the left hand side

        10x2 - 13x - 3  =  0

There are two ways of completing this problem.  The first is to use the quadratic formula

        a  =  10    b  =  -13    c  =  -3

       

Hence

                13 + 17
        x =                   
                   20    

or

                13 - 17
        x =                   
                   20    

We get  x  =  3/2    or   x  =  -1/5

 

Alternatively, we can factor using the AC method:

        AC  =  -30

The two numbers that multiply to -30 and add to -13 are

        (-15,2)

We now rewrite

        10x2 - 13x - 3  =  10x2 - 15x + 2x - 3

        =  5x(2x - 3) + 1(2x - 3)        Factoring by grouping

        =  (5x + 1)(2x - 3)  =  0

Hence

        5x + 1  =  0     or       2x - 3 = 0

        x  =  -1/5    or    x  =  3/2

 

B)   2x2 + 15 = 11

Solution

        To solve this, there is no "x" term, so we can use the square root property:

        2x2  =  -4        Subtracting 15 from both sides

        x2  =  -2        Dividing both sides by two

        x  =  i        Taking the square root of both sides and pulling out an i

 

Problem 7:  

Solve the following by completing the square

   5x2 - 20x + 21  =  0

Solution

        5(x2 - 4x)  + 21  =  0        Pulling out the 5 from the first two terms

Now calculate the magic number (b/2)2

        (-4/2)2  =  (-2)2  =  4

        5(x2 - 4x + 4 - 4)  + 21  =  0        Adding and subtracting the magic number 4

        5[(x - 2)2 - 4] + 21  =  0        Factoring the first three terms

        5(x - 2)2 - 20 + 21  =  0        Distributing the 5 through

        5(x - 2)2 + 1  =  0        Adding the numbers

        5(x - 2)2  =  -1        Adding the numbers

        (x - 2)2  =  -1/5        Dividing both sides by 5

        x - 2  =  i /        Taking the square root of both sides and pulling out an i

        x  =  2 i /        Adding 2 to both sides

        x  =  2 i/5        Rationalizing the denominator

 

 

Problem 8: 

Solve the following using the quadratic formula 

        6x2 + 5x - 4  =  0 

 

Solution

We use the quadratic formula with

        a  =  6,    b  =  5,    c  =  -4

       

So that 

        x   =   1/2  +  11/12         or        x   =   1/2  -  11/12   

Notice that we could have instead used the AC method to factor.

 

 

 

Problem 9  Simplify the expression.  Assume all variables represent positive real number.

         

Solution

       

 

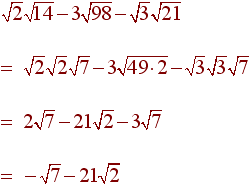
Problem 10  Multiply and Simplify

       

   Solution

               

 

Problem 11  Rationalize the denominator

             5
                       
          4 -

 Solution

                     5    (4 + )
                                                
                 ( 4 - )(4 + )

 

                      20 + 5
             =                          
                        16  -  6

 

                      20 + 5
             =                          
                            10

 

Problem 12  Simplify

       

 Solution

       

 

Problem 13  Solve the equation

       

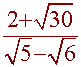
Solution

First isolate the first root by adding the square root of x to both sides.

       

Next square both sides.  Do not forget to FOIL out the right hand side.

       

Now isolate the square root of x.  Subtract x + 9 from both sides to get

       

Divide by -6:

       

Finally square both sides to get

        x  =  1

Put x = 1 back into the original equation to see if it works:

       

So x = 1 is the solution.

 

 

Problem 14  Solve the compound inequality

        2x - y > 4

        2x + 3y < 6

Solution

Graph the two lines first.  Notice that the first should be graphed as a dashed line, since the sign is a ">" so equality makes it false.  The second will be a solid line, since equality makes is true.  We construct two T-tables

 
x y
0 -4
2 0
 
x y
0 2
3 0

Now graph the two lines:

       

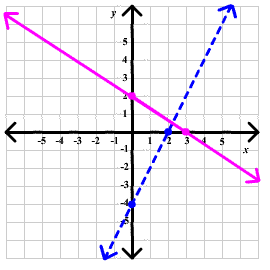
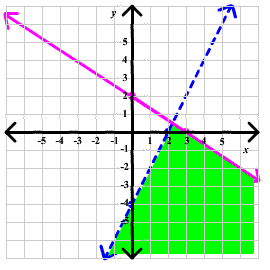
Now we use the origin as a test point for both lines.  For the blue line, we have

        2(0) - 0  >  4

is false so we include points below the blue line

For the pink line, we have

        2(0) + 3(0)  <  6

is true, so we include points below the pink line.  Below is the graph of the solution.

       

 

Back to the Factoring and Rational Expressions Page

Back to the Basic Algebra Part II Page

Back to the Math Department Home Page

Questions, Comments and Suggestions  Email:  greenl@ltcc.edu