Practice Exam 1

Practice Exam 1

Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.

Problem 1 Use the method of elimination to solve the system. Then graph the system to check your solution.

-3x + 2y = 6
9x - 6y = 36

Solution

We multiply the first equation by 3 and add

-9x + 6y = 18
9x - 6y = 36

0 = 54

This is a contradiction, so there is no solution.

To graph it we have make T-Tables as shown below

x y

0 3

-2 0

x y

0 -6

4 0

The graphs are shown below. Notice that they are parallel.

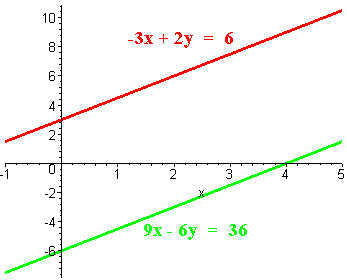
5x + 3y = 15
3x - 2y = 28

Solution

Multiply the first equation by 2 and the second by 3 and add

10x + 6y = 30
9x - 6y = 84

19x = 114
x = 114/19 = 6

Now substitute this value into the second equation (the first will work also) to get

3(6) - 2y = 28

18 - 2y = 28

-2y = 28 - 18 = 10

y = 10/-2 = -5

The solution is (6, -5).

To graph it we have make T-Tables as shown below

x y

0 5

3 0

x y

0 -14

28/3 0

The graphs are shown below. Notice that the lines intersect at (6,-5).

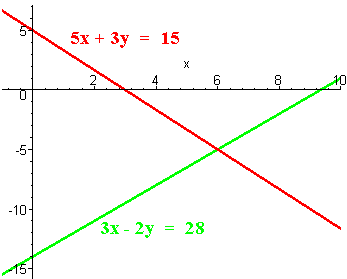
Problem 2 Use the method of substitution to solve the system. Then graph the system to check your solution.

7x + y = 3
4x + 3y = -8

Solution

We solve the first equation for y:

y = 3 - 7x

Now plug this into the second equation:

4x + 3(3 - 7x) = -8

4x + 9 - 21x = -8

9 - 17x = -8

-17x = -17

x = 1

Now plug in x = 1 in the equation

y = 3 - 7(1) = -4

Hence the solution is (1,-4).

To graph it we have make T-Tables as shown below

x y

0 3

3/7 0

x y

0 -8/3

-2 0

The graphs are shown below. Notice that the lines intersect at (1,4).

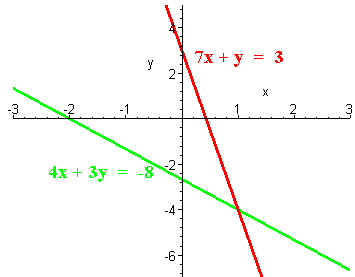
y = 3x - 2
6x - 2y = 4

Solution

We can substitute the first equation into the second:

6x - 2(3x - 2) = 4

6x - 6x + 4 = 4

4 = 4

This is an identity, hence there are an infinite number of solutions (all points lying on the line y = 3x - 2). Notice the the y-intercept is -2 and the slope is 3. We can draw the point (0,-2) and rise 3 and run 1 from this point to graph the line.

Problem 3 Last year, you inherited $30,000 from a distant relative. You took the money and invested some of it in a bank account that paid 2% interest and invested the rest in stocks that increased 6%. The total earnings on the invested money was $900. How much money was invested in the bank account and how much was invested in the stock market? Show the equations that you set up and how you either used substitution or elimination to solve the system.

Solution

Since we want to find out how much money was invested in each account, this guides towards the variables:

Let x = the amount of money invested in the 2% account.

Let y = the amount of money invested in the 6% accruing stocks.

Since the total invested was $30,000, we have the equation

x + y = 30,000

The total earnings was $900. The contribution from the bank was 2% of the amount in the bank or 0.02x. The Contribution from stocks was 6% of the amount in stocks or 0.06y. We now have the equation

0.02x + 0.06y = 900

If you do not like decimals, you can multiply all three terms by 100 to get

2x + 6y = 90,000

We can solve for y in the first equation to get

y = 30,000 - x

Now substitute the into the previous equation to get

2x + 6(30,000 - x) = 90,000

2x + 180,000 - 6x = 90,000

-4x + 180,000 = 90,000

-4x = -90,000 subtracting 180,000 from both sides

x = -90,000/-4 = 22,500

Plugging 22,500 back in gives:

y = 30,000 - 22,500 = 7,500

We can conclude that you invested $22,500 in the bank and $7,500 in stocks.

Problem 4 You own a non-profit theater that has 2,000 seats. In order to break on even Saturday's concert you must collect a total of $24,000 from the ticket sales. You have decided to partition the theater's seats into "premium seats" which you will sell for $30 per seat and "general admission" seats which you will sell for $10 per seat. If you are certain the tickets will sell out, how many seats should you sell as "premium seats"? Show the equations that you set up and how you either used substitution or elimination to solve the system.

Solution

Since we want to know about how many seat of a certain type there are, we have the variables:

Let x = The number of premium seats.

Let y = The number of general admission seats.

Since the total number of seats is 2000, we have the equation

x + y = 2000

The ticket sales from the premium seats will be $30 times the number of premium seats, x or 30x. The ticket sales from the general admission seats will be $10 times the number of general admission seats, y or 10y. Since the total ticket sales will be $24,000, we have the equation

30x + 10y = 24,000

Solving the first equation for y gives

y = 2000 - x

Plugging this into the second equation gives

30x + 10(2000 - x) = 24,000

30x + 20,000 - 10x = 24,000

20x + 20,000 = 24,000

20x = 4000 Subtracting 20,000 from both sides

x = 4000/20 = 200

Plugging 200 back in gives

y = 2000 - 200 = 1800

Hence you should have 200 premium seats and 1,800 general admission seats.

Problem 5 Graph the system of inequalities below.

3x + 5y < 15
y > 2x + 1

Solution

First we graph the equalities by making T-Tables.

x y

0 3

5 0

x y

0 1

-1/2 0

The graphs are shown below. Note that both lines are dashed since the inequality signs do not have equalities.

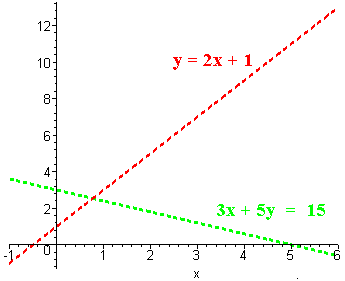
Now we use the origin (0,0) as the test point for each line. We have

3(0) + 5(0) < 15 or 0 < 15

is a true statement, hence we shade the side of the green line that includes (0,0). That is we shade the part of the plane below the green line. Next we have

(0) > 2(0) + 1 or 0 > 1

is a false statement, hence we shade the side of the red line that does not include (0,0). That is, we shade the part of the plane above the red line. The solution is the part of the plane that below the green line and above the red line as shown below.

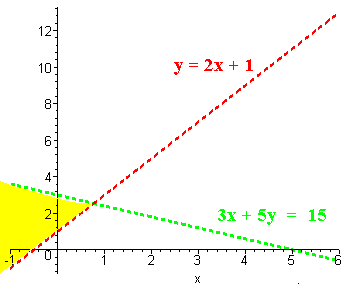
Problem 6

Consider the system of inequalities below.

        y > -1
        x + y < 4
        x - y < 3

Write the coordinates of the plotted points below that are solutions of this system.

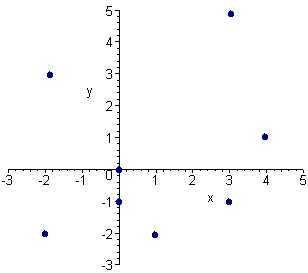
Solution

We first graph the lines on top of the above graph making the first line solid since is has the ">" sign and the second two dashed since it does not have equality.

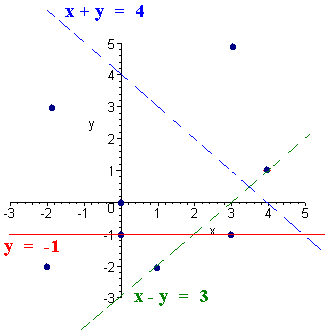
Now test the origin, (0,0) for inclusion. We have

(0) > -1

is a true statement, so we include the origin and the part above the red line is shaded. We have

(0) + (0) < 4

is also a true statement, so we include the origin and the part below the blue line is included. We have

(0) - (0) < 3

is also a true statement so we include the origin and the part above the green line is included. We shade in this region and circle the points in the shaded region.

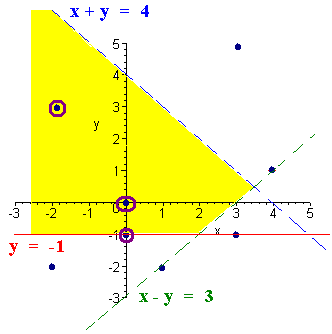
The three shaded points have coordinates (-2,3), (0,0), and (0,-1).

Problem 7 Factor

15x²y³ - 18xy⁴ + 21x⁴y²

Solution

We see that the greatest common factor (GCF) of the three terms is 3xy². We pull the GCF from all three terms to get

3xy²(5xy - 6y² + 7x³)

Problem 8 Factor

6x² + 9x - 10x -15

Solution

We can factor by grouping. We group

(6x² + 9x) + (-10x - 15)

Now pull out the GCFs of 3x and -5 respectively.

3x(2x + 3) - 5(2x + 3)

Now factor out the x + 3 to get

(2x + 3)(3x -5)

Problem 9 Factor

x² - x - 6

Solution

We need to find two numbers that multiply to -6 and add to -1. The factors of -6 are (1,-6), (2,-3), (-3,2), (-6,1), (-1,6), (-2,3), (-3,2), and (-6,1)

We see that (-3,2) works, hence we can factor it as

(x - 3)(x + 2)

Problem 10 Solve

6x² + x - 15 = 0

Solution

We use the AC method. We have

AC = (6)(-15) = -90

Now we seek two numbers that multiply to -90 and add to 1. These numbers are 10 and -9. Now we break up the x into

x = 10x - 9x

and substitute

6x² + 10x - 9x - 15 = 0

Now factor by grouping

(6x² + 10x) + (-9x - 15) = 0

Pull out the GCFs

2x(3x + 5) - 3(3x + 5) = 0

Now pull out the 3x + 5

(3x + 5)(2x - 3) = 0

Now use the zero product rule

3x + 5 = 0 or 2x - 3 = 0

3x = -5 or 2x = 3

x = -5/3 or x = 3/2