Solving Systems of Equalities and Inequalities, and More Word Problems

Systems of Equations

We define a linear system of two equations in two unknowns by

ax + by = c

dx + ey = f

The geometry of a 2 by 2 linear system is that of two lines. If the lines are parallel (same slope) then they will not intersect. Otherwise the solution of the 2 by 2 linear system is the intersection point.

Elimination

One way of solving systems of linear equation is called substitution.

Step by Step method:

Step 1: Line up the equations so that the variables are lined up vertically.
Step 2: Choose the easiest variable to eliminate and multiply both equations by different numbers so that the coefficients of that variable are the same.
Step 3: Subtract the two equations.
Step 4: Solve the one variable system.
Step 5: Put that value back into either equation to find the other equation.
Step 6: Reread the question and plug your answers back in to check.

Example

Solve

2x = 3y + 3

4x - 5y = 7

Solution

2x - 3y = 3
4x - 5y = 7
Multiply the first equation by 2.
4x - 6y = 6
4x - 5y = 7
-y = -1 After subtracting the equations.
y = 1
        4x - 5(1) = 7        Substituting 1 for y in the second equation.
        4x = 12
        x = 3
The answer is (3,1)
We see that
2(3) = 3(1) + 3
4(3) - 5(1) = 7

Exercises

Solve:

y = 5x - 5
3x + 4y = 26
y = 4x + 2
8x - 2y = -3

Substitution

There is a second way to solve such systems. We call this alternative way substitution.

Step by step method

Step 1: Solve for one variable explicitly in terms of the other. Box this equation.
Step 2: Substitute this into the other equation.
Step 3: Solve what you get.
Step 4: Substitute this result into the expression in the box.
Step 5: Check the solution.

Example

Solve

x - 2y = 2

3x - 5y = 7

Solution

We can manipulate the first equation to get x by itself.

x = 2 + 2y
3(2 + 2y) - 5y = 7 Substituting into the second equation.
        6+ 6y - 5y = 7
        6 + y = 7
        y = 1
x = 2 + 2(1) = 4 Plugging back into the equation from step 1.
The solution is (4,1)
We check:

4 - 2(1) = 2

and

3(4) - 5(1) = 7

Exercises

Solve using the method of substitution.

3x + y = 5

2x - 3y = -4
5x - 4y = 2
8x + 5y = 26

Solving Systems of Inequalities

Last time, we solved inequalities. If we have a system of inequalities, we follow the same steps except this time we graph all of the inequalities and take the intersection of the defined regions.

Example

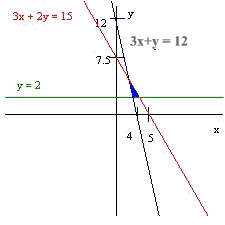
Graph the system of inequalities:

3x + y > 12

3x + 2y < 15

y > 2

Solution

We draw T-tables to graph the two lines. Note that the last two lines is horizontal.

3x + y = 12

x y

0 12

4 0

3x + 2y = 15

x y

0 7.5

5 0

We solve the two by two system to find the coordinates of the intersection.

y = 12 - 3x

3x + 2(12 - 3x) = 15

3x + 24 - 6x = 15

-3x = -9

x = 3

Plugging back in

y = 12 - 3(3) = 3

Hence the point (3,3) is the point of intersection.

The graph is shown below.

Exercises:

Graph:

x - y > 2
y - x > -1
3x + 2y > 15
x > 3

Problem Solving

Example

How many grams of pure gold and how many grams of an alloy that is 55% gold should be melted together to produce 72 g of an alloy that is 65% gold?

Let

x = grams of pure gold

y = grams of the alloy.

Then

x + y = 72

and

x + .55y = .65(72) = 46.8

Hence

x = 72 - y

(72 - y) + .55y = 46.8

72 - .45y = 46.8

-.45y = -25.2

y = 56

Solving gives

y = 56

Now put this into the "boxed" equation to find x.

x = 72 - 56 = 16

Approximately 16 grams alloy and 56 grams of pure gold need to be used in order to have 72 g of .55 alloy.

Graph of y < x y < 1

Back to the Quadratic Functions and Linear Inequalities Page

Back to the Basic Algebra Part II Page

Back to the Math Department Home Page

e-mail Questions and Suggestions