Slope

I.  Return Quiz III

II.  Homework

III.  Lines and Slope

The class will get together and discuss the definition of a line.  

Definition:  Let (x₁,y₁) and (x₂,y₂) be two points then the slope for those two points is rise/run or

m = (y₂ - y₁)/(x₂ - x₁)

Example:  For the points (1,2) and (5,-3) we have

m = (-3 - 2)/(5 - 1) = -5/4

Definition:  A line through a point P  with slope m is the collection of points Q such that the slope between P and Q is m.

Example:  Sketch the line through the point (1,-1) with slope  m = 2.  This will be done in class.  We plot the point (1,-1) and rise 3 and run 1 from (1,-1) arriving at (2,2).  Then we connect the dots.

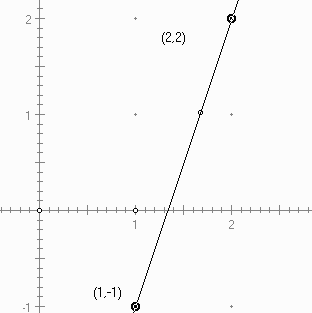
Exercise:  Sketch the line through the point (2,-3) with slope 1/2.

III.  Special Cases

Vertical lines have an undefined slope and horizontal lines have a zero slope

Example:  Without graphing, describe the line through

A.  (3,5) (3,2)

B.  (1,2) (-3,2)

Solution:  

A.  We compute the slope:  m = (2 - 5)/(3 - 3) = -3/0 which is undefined, hence the line is vertical

B.  We compute the slope:  m = (2 - 2)/(-3 - 2) = 0/-5 = 0 hence the line is horizontal.

Exercise:  Determine Whether the points (1,1), (2,4), and (7,9) are colinear.