Relations, Functions, and Function Notation

I.  Homework

II.  Definition of a Relation, Domain, and Range

Examples:

A)  Consider the relation that sends a student to that student's age.

B)  Consider the relation that sends a student to the courses that student is taking

C)  Consider the relation that sends a parent to the parent's child.

Definition:

A relation is a correspondence between two sets (called the domain and the range) such that to each element of the domain, there is assigned one or more elements of the range.

Non-Example:  Let the domain be the set of all LTCC students and the range be the set of all math course offerings at LTCC.  Then the map that takes a student and sends the student to the math course he or she is taking is not a relation since there are students who are not taking math courses.

To state a relation, one must state the domain and the range and the rule.

Example:  

(2,3), (2,4), (3,7), and (5,2) is a relation with

Domain:  {2,3,5} and

Range:  {2,3,4,7}

A circle represents the graph of a relation.

III.  Functions

Definition:  

A function is a correspondence between two sets (called the domain and the range) such that to each element of the domain, there is assigned exactly one element of the range.

(each input has a unique output)

Examples:

(3,3), (4,3), (2,1), (6,5) is a function with domain: {2,3,4,6} and range {1,3,5}

(2,1), (5,6), (2,3), (6,7) is not a function since 2 gets sent to more than one place.

IV.  The Vertical Line Test

If any vertical line passes through a graph at more than one point, then the graph is not the graph of a function.  Otherwise it is the graph of a function.  

Examples:

A circle is not the graph of a function

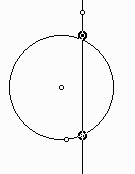
A (non-vertical) line is the graph of a function.  

Other examples will be given in class.

V.  Function notation

We write f(x) to mean the function whose input is x.

Examples:

If f(x) = 2x-3

then f(4) = 2(4) - 3 = 5

We can think of f and the function that takes the input multiplies it by 2 and subtracts 3.  Sometimes it is convenient to write f(x) without the x. Thus:

f( ) = 2( ) - 3

whatever is in the parentheses, we put inside.  For example:

f(x - 1) = 2(x - 1) - 3

(f(x + 4) - f(x))/4 =  ([2(x + 4) - 3] - [2(x) - 3]/4 = (2x + 8 - 3 - 2x + 3)/4 = 8/4 = 2

We will try other examples.

VI.  Function Arithmetic

We define the sum, difference, product and quotient of functions in the obvious way.

Example:

If f(x) = (x + 1)/(x - 1) and g(x) = x² + 4

then

(f + g)(x) = (x + 1)/(x - 1)  + (x² + 4)

(f - g)(x) = (x + 1)/(x - 1)  - (x² + 4)

(f g)(x) = [(x + 1)/(x - 1)][(x² + 4)]

(f /g)(x) = [(x + 1)/(x - 1) ]/ (x² + 4)