Money, Mixture, Motion, and Inequalities
Example
You have 40 coins in nickels and dimes. How many dimes
do you have if you have a total of $2.85?
Solution:
Our answer is
"We have ____ dimes"
Let
d = the number of dimes you
have
then
40 - d =
the number of nickels that you have.
The total money that you have is
10d + 5(40 - d)
= 285
Value of dimes + Value of nickels
= 285
10d + 200 - 5d = 285 Distributing the 5
5d + 200 = 285 10d - 5d = 5d
5d = 85 Subtracting 200 from both sides
d = 17
Dividing by
5
We have 17 dimes.
Example
You are the manager of the new Tahoe Stadium. You sell your VIP seats
for $200 each and your general admission seats for
$75. Your stadium
holds 10,000 people, and you need to earn at least $1,000,000. If
you sell out, how many of your seats should you designate as VIP seats?
Solution:
Our answer should be
"We should designate ________ as
VIP seats."
Let
x =
number of VIP seats
then
10,000 - x =
number of general admission seats.
The money from the VIP seats is
200x
and the money from the general admission seats is
75 (10,000 - x)
Hence
200x + 75(10,000 - x) = 1,000,000 VIP money + general Ad money = 1,000,000
200x + 750,000 - 75x = 1,000,000 Distributing the 75
125x + 750,000 = 1,000,000 200x - 75x = 125x
125x = 250,000 Subtracting 750,000
x = 2,000 Dividing by 125
We designate 2,000 seats as VIP seats.
Example
Vodka contains 40% alcohol and wine contains 10% alcohol. You want
to make a new drink that is 20% alcohol using vodka and wine. How much
of each should you use to make 15 ounces of this drink?
Solution:
Our answer should be
"Use _______ ounces of vodka
and _________ ounces of wine.
We let
x =
number of ounces of vodka
Then
15 - x
is the number of ounces of wine
Note that the amount of alcohol in the final mixture is
15
(0.2) = 3
15 ounces times
20% alcohol =
3
Hence we can write
0.4x + 0.1(15 - x)
= 3 vodka alcohol + wine alcohol = total alcohol
Multiplying by 10 to get rid of the
decimal, we get:
4x + (15 - x) = 30
4x + 15 - x = 30
3x = 15 4x - x = 3x and 30 - 15 = 15
x = 5 dividing by 3
Hence we pour 5 ounces of vodka and 10 ounces of wine. (It is not recommended to try this at home).
Example
Suppose that I am walking from school at 3 miles per hour and start at
12:00.
At 12:30, you start riding your bike at 18 miles per hour to find me.
At what time do you find me?
Solution:
The answer is
"You find me at _______"
Let
t = the time after
12:00
We use the formula
distance = rate times time
Then my distance from school is
3t
To find your distance from school, multiply the rate, 18
by the time since you left, t - 1/2.
18 (t - 1/2)
We set the two equal to each other:
3t =
18(t - 1/2)
3t =
18t - 9
distributing through
-15t =
-9
subtracting 18t from both sides
t =
9/15 = 3/5 = 36/60 or 36
minutes. dividing both sides by
-15
Hence you find me at 12:36.
Linear Inequalities
Definition A linear inequality is one that can be reduced to
ax + b < 0 |
Step by step method for solving linear inequalities:
-
Simplify both sides (distribute and combine like terms).
-
Bring the x's to the left and the constants to the right.
-
Divide by the coefficient (changing the inequality if the sign of the inequality is negative).
-
Plot on a number line (remember holes and dots).
Example
Solve
2(x - 9) <
3(2x - 10)
Solution
2x - 18 < 6x - 30 Distributing the 2 and the 3
-4x < -12 Subtracting 6x and adding 18
x > 3 Dividing by 4
Plot on a number line with a hole at 3 and an arrow to the right of 3.
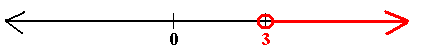
To play with the number line go to
Inequality
Play
Exercises
-
3x - 5 > 6(x - 1)

-
5(x + 2) < 2(x - 3)

Back to the Math Department Home
e-mail Questions and Suggestions