Linear Equations and Word Problems
Algebraic Expressions
We will define the term variable which is analogous to a pronoun in grammar.
|
Definition A variable is a symbol that represents a number that may change depending on the circumstance. |
Examples
We often use the variable t to represent time. We can
use the variable h to represent height. We use the letter
x for the
variable when the variable stands for a general number without context.
Definition A constant is a symbol that represents a known fixed number. |
Examples
c = 3 x 108
p
= 3.14...
|
Definition An algebraic expression is an expression consisting of constants, variables, and symbols of operators. |
Examples
-
m c2
-
p r2
3x2 +2x - 1
|
Definition A term is an expression that is related by addition or subtraction. |
Example
In
3x2 +2x -
1
3x2
2x and
1
are the three terms. 3, 2,
-1 are called
the coefficients of
x2, x, and
1 respectively. We say two
terms are like terms if they differ only in their coefficient.
Example
3x2
and
5x2
are like terms. We can add like terms by adding their coefficients.
3x2 + 5x2
= 8x2
Exercise
Simplify the expression
5x2
- 2p + 3x2 + 5s2 + 2p -
3(2x2 -3s2)
![]()
Linear Equations
Recall that an expression is a statement involving x's, constants, and operators.
An expression is like the subject of a sentence. An equation
is more like a complete sentence which as a subject, verb and predicate.
The verb will typically be an "= " sign.
Example
3x + 1 = 4
is an example of an equation.
When we have an equation, we can attempt to solve it that is to find which x values
satisfy the equation. An x value satisfies an equation if when we
substitute the value in the equation for x, the equation is true. To solve for the variable
x means that we have an equation of the form.
x = a number.
The set of all x that satisfy the equation is called the solution
set of the equation.
To solve we isolate x by
-
Use the distributive property.
-
Combine like terms.
Subtract all the x terms from the right hand side- "Do unto the left as you would do unto the right."
-
Subtract all the constant terms from the left hand side.
-
Divide by the coefficient in front of x.
Example:
Solve the following equation for x.
3(2x - 1) + 4x =
2(4x + 2)
Solution:
-
6x - 3 + 4x = 8x + 4
-
10x - 3 = 8x + 4
-
2x - 3 = 4
-
2x = 7
-
x = 7/2
|
Definition: An equation that is true for some x but not for others is called a conditional equation. The value of x that makes the equation true is called the solution of the equation. |
In the above example
we say that
x = 7/2
is a solution to the equation.
Example
Solve
3(2x - 1) - 2(3x + 1) = 0
Solution
6x - 3 - 6x - 2
= 0 (Distributed the
3 and the 2)
0 - 5 = 0
-5 = 0
Since this can never happen we say that the equation is a contradiction.
Example:
Solve
2(x - 3) - 2x + 8 = 2
Solution:
2x - 6 - 2x + 8
= 2 (Distributed the
2)
0 + 2 = 2 (Combined the 2x - 2x and the -6 + 8)
2 = 2
Since this is always true, we say that the equation is an identity.
Problem Solving With Formulas
A formula is an equation that relates real world quantities.
Examples
P =
2l + 2w
is the formula for the perimeter P of a rectangle given the length
l and width w.
d =
rt
is the formula for the distance traveled d given the speed
s
and the time t.
A =
P + Prt
is the formula for the amount A in a bank account
t years after
P dollars is put in at an interest rate of r.
V = pr2h
is the formula for the volume V of a cylinder of radius
r and height h, where p @ 3.14.
h
A =
(b1 + b2)
2
is the formula for the area A of
a trapazoid with height h and bases b1 and
b2.
We say that a formula is solved for a variable x if the equation becomes
x =
stuff
where the left hand side does not include any x's.
Example
Solve
C = 2pr
for r then determine the radius of a circle with circumference
4.
Solution
Divide both sides by 2p:
C
= r
2p
Use the reflexive property to get
C
r =
2p
Now plug in 4 for C to obtain
4
2
r =
=
2p
p
|
Steps for Solving a Word Problem
|
Example:
A pile of sand has the shape of a right circular cone.
Find the height of the pile if it contains 100 cc of sand and the radius
is 5 cm.
Solution:
-
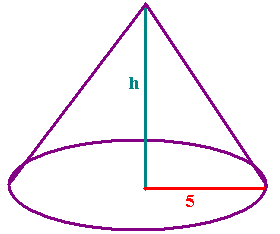
-
The height of the pile is ________ cm.
-
We use the formula for the volume of a right circular cone:
V = 1/3 pr2h.
-
Multiply by 3 on both sides to get
3V = pr2h.
Divide both sides by pr2 to obtain
3V 3V
pr2 pr2
-
3(100) 12
h =
p52 p
-
The height of the pile is 12/p cm.
e-mail Questions and Suggestions