Practice Exam 1
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1 Simplify the following expressions.
A. |-7|2 - |33|
Solution
|-7|2 - |33| = 72 - 33 = 49 - 27 = 22
B. 37 - 18 - (-11)
Solution
37 - 18 -(-11) = 19 - (-11) = 19 + 11 = 30
C. (7 + 11) ÷ 6 - 2
Solution
(7 + 11) ÷ 6 - 2 = 18÷ 6 - 2 = 3 - 2 = 1
D. -42 + (-4)2
Solution
Notice that for the first term the order of operations tell us that the "-" is performed after the square and for the second term the parentheses force the negative to be performed before the square. We have
-(4)(4) + (-4)(-4) = -16 + 16 = 0
E. 2(2x - 3) + 3(4 - x)
Solution
2(2x - 3) + 3(4 - x) = 4x - 6 + 12 - 3x
= 4x - 3x - 6 + 12 = x + 6
F. 2x(x - 3) + 5(3x + 1)
Solution
Use the distributive property
(2x)(x) + (2x)(-3) + 5(3x) + (5)(1)
= 2x2 - 6x + 15x + 5
= 2x2 + 9x + 5
6x + 3
G.
3
Solution
Notice that the 3's do not cancel, since there are two terms in the numerator. Instead, we split the numerator:
6x
3
+
= 2x + 1
3
3
H. 0.3(x + 4) - 0.1(x + 2)
Solution
Use the distributive law:
0.3x + (0.3)(4) - 0.1x - (0.1)(2) = 0.3x + 1.2 - 0.1x - 0.2
= 0.2x + 1
Problem 2 Evaluate the following expression when x = 2, y = -1, and z = 3
x3y - 4y2 +2xz -3z + 2
Solution
We have
(2)3(-1) - 4(-1)2 + 2(2)(3) - 3(3) + 2
= (8)(-1) - (4)(1) + 12 - 9 + 2
= -8 - 4 + 12 - 9 + 2
= -12 +12 - 9 + 2
= 0 - 9 + 2
= -9 + 2
= -7
Problem 3 Give the name of the property that the following identity uses.
A. (2x + 3) + y = 2x + (3 + y)
Solution
This is the associative property of addition, since we are just regrouping.
B. z + (3 - x) = (3 - x) + z
Solution
This is the commutative property of addition since we are changing the order of the terms.
Problem 4
Solve the following equations. Then identify each as a conditional equation, an inconsistent equation, or an identity.
A. 3x - 5 = 4x
Solution
We subtract 3x from both sides
3x - 5 = 4x
-3x
-3x
________________
-5 =
x
x = -5 This is a Conditional Equation
B. 5(x - 3) - (x + 5) = 4x - 1
Solution
First distribute
5x - 15 - x - 5 = 4x - 1
Combine like terms
4x - 20 = 4x - 1
-4x + 20 -4x + 20
__________________________
0 = 19
This is an inconsistent equation (No Solution)
x
2x
C. 3 +
=
3
5
Solution
Multiply all three terms by the common denominator 15
(15) x
(15)2x
(15) 3 +
=
3
5
45 + 5x = 6x
-5x -5x
_________________
45
= x
x = 45
This is a conditional equation.
x
x
x
D. 1 -
+
=
+ 1
4
2
4
Solution
Multiply all five terms by the common denominator 8
(8)x
(8)x (8)
x
(8)1 -
+
=
+ (8)1
4 2 4
8 - 2x + 4x = 2x + 8
8 + 2x = 2x + 8
This is an identity.
Problem 5
Translate each verbal expression into an algebraic expression with one variable:
A. 3 less than twice a number
Solution
Twice a number can be represented by 2x. Three less than this is
2x - 3
B. The area of a rectangle given that the width is 5 meters more than the length.
Solution
If L is the length of the rectangle, then the width is 5 + L. The area is the product of the length and the width.
Area = L(5 + L)
C. The product of two consecutive even numbers is 168.
Solution
If the first number is x then the next even number is x + 2. their product is x(x + 2). We can now write
x(x + 2) = 168
Problem 6
Determine whether the given number is a solution to the equation following it
A. -6, -x + 5 = 11
Solution
We plug in (-6) where we see an x:
-(-6) + 5 =? 11
6 + 5 =? 11
Yes x = -6 is a solution to the equation.
x - 4
B. 2,
= 3
x + 1
Solution
We plug in (2) where we see an x:
(2) - 4
=? 3
(2) + 1
-2
=? 3
3
Since the left hand side does not equal the right hand side, we can conclude that x = 2 is not a solution to the equation.
Problem 7
A window that is in the shape of a triangle has it largest side four times as long as its shortest side. The middle length side is three times as long as the shortest side. If the perimeter of the triangle is 40 inches, what are the dimensions of the triangle?
Solution
First sketch the picture letting x be the length of the shortest side.
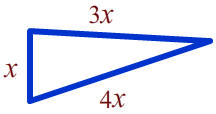
Notice that since the shortest side is of length x, the longest side has length 4 times that or 4x. Similarly, the middle length side has length 3x.
The perimeter is the sum of the side of the triangle and its length is 40 inches. Hence
x + 3x + 4x = 40
Now combine like terms:
8x = 40
Divide both sides by 8 to get
x = 5
Finally, answer the question. The triangle's shortest side is 5 inches long, the longest side is 20 inches long, and the middle length side is 15 inches long.
Problem 8
Los Angeles is 400 miles from Sacramento. If Sue leaves Sacramento at 10:00 AM and averages 75 miles an hour, when will she arrive in Los Angeles?
Solution
We use the distance = rate times time formula. We have
d = 400 and r = 75
Thus
400 = (75)(t)
Now divide both sides by 75 to get
t = 400/75 = 5 1/3
Notice that 1/3 of an hour is 20 minutes. Since Sue started out at 10:00 AM, you can add five hours and 20 minutes to that time and get that Sue will arrive in Los Angeles at 3:20 PM.
Problem 9
Solve the inequality. Graph the solution set and write the solution in interval notation.
5 - 3x > 1 - x
Solution
Add x and subtract 5 from both sides to get
-2x > -4
Next divide both sides by -2. Remember that when we divide by a negative number, the inequality is switched.
x < 2
The graph is shown below. Notice that since the inequality is "<" and not "<" we use an open circle instead of a closed circle.
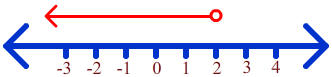
Next writing in interval notation, remembering to use "(" and ")" to indicate that we are not including the endpoints.
![]()
Problem 10
Solve the inequality. Graph the solution set and write it in interval notation.
-9 < 3(x - 1) < 0
Solution
First divide all three terms by 3 to get
-3 < x - 1 < 0
Now add 1 to all three sides to get
-2 < x < 1
We can graph this on the number line as shown below.

Now write this in interval notation remembering to use "(" for not including the endpoint and "]" for including the endpoint
(-2,1]
e-mail Questions and Suggestions