Practice Exam 1

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Problem 1  Simplify the following expressions.

A.  |-7|² - |3³|

Solution

|-7|² - |3³|  =  7² - 3³  =  49 - 27 = 22

B. 37 - 18 - (-11)

Solution

        37 - 18 -(-11)  =  19 - (-11)  =  19 + 11  =  30

C.  (7 + 11) ÷ 6 - 2

Solution

        (7 + 11) ÷ 6 - 2  =  18÷ 6 - 2   =  3 - 2  =  1

D.  2(2x - 3) + 3(4 - x)

Solution

        2(2x - 3) + 3(4 - x)  =  4x - 6 + 12 - 3x

        =  4x - 3x - 6 + 12  =  x + 6

Problem 2  Evaluate the following expression when x = 2, y = -1, and z = 3

     x³y - 4y² +2xz -3z + 2

Solution

We have

        (2)³(-1) - 4(-1)² + 2(2)(3) - 3(3) + 2

        =  (8)(-1) - (4)(1) + 12 - 9 + 2

        =  -8 - 4 + 12 - 9 + 2

        =  -12 +12 - 9 + 2

        =  0 - 9 + 2

        =  -9 + 2

        =  -7

Problem 3  Give the name of the property that the following identity uses.

A.  (2x + 3) + y  =  2x + (3 + y)

Solution

This is the associative law of addition, since we are just regrouping.

B.  z + (3 - x)  =  (3 - x) + z

Solution

This is the commutative law of addition since we are changing the order of the terms.

Problem 4

A.  Solve the following for x.

          3x + y  =  x - 2

Solution

Subtract x from both sides

        3x - x + y  =  x - x - 2

        2x + y  =  -2

Subtract y from both sides

        2x + y - y  =  -2 - y

        2x  =  -2 - y

Divide by 2 on both sides

        x  =  -1 - y/2

B.  Einstein's famous equation relates the energy (E) produced by annihilating a mass m.  If c is the speed of light, then

          E  =  mc² 

Solve this equation for m.

Solution

We just divide by c² on both sides

        E
                =  m
        c²

or

                 E
      m  =           
                 c²

Problem 5

One number is 8 less than twice the other number.  The sum of the two numbers is 31, find the two numbers.

Solution

Let

        x = the first number

then

        2x - 8  =  the second number

so that

        x + (2x - 8)  =  31

        3x - 8  =  31

Now add 8 to both sides

        3x  =  39

Divide by 3 to get

        x  =  13

The second number is

        2x - 8  =  2(13) - 8  =  26 - 8  =  18

Problem 6

The length of a rectangle is 18 inches less than three times its width.  The perimeter of the rectangle is 52 inches.  Find the dimensions of the rectangle.

Solution

We draw the picture below

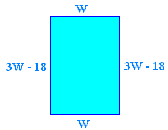
We let

        W  =  the width of the rectangle

then

        3W - 18  =  the length of the rectangle

The perimeter is the sum of twice the length and twice the width.

        2(3W - 18)  + 2W  =  52

        6W - 36 + 2W  =  52

        8W - 36  = 52

Now add 36 to each side.

        8W  =  88

Next divide by 4 to get

        W  =  11

so that the length is

        3(11) - 18  =  33 - 18  =  15

The rectangle has width 11 and length 15.

Problem 7

To buy your $25,000 car, you had to get loans from two different sources for the $25,000.  The first source charged 6% interest and the second source charged 8% interested per year.  If the total amount of interest that you will pay for the first year is $1800, how much did you borrow from each source?

Solution

Let x = the loan amount at 6% interest

      25000 - x  =  the loan amount at 8% interest

Then

        0.06x + 0.08(25000 - x)  =  1800

Multiply by 100 to clear the decimals:

        6x + 8(25000 - x)  =  180000

Now distribute the 8

        6x + 200000 - 8x  =  180000

Combine like terms to get

        -2x + 200000 =  180000

Subtract 200000 from both sides to get

        -2x  =  -20000

Now divide by -2

        x  =  10000

We can conclude that the loan amount at 6% was $10,000 and the loan amount at 8% interest was $15,000.

Problem 8  Solve the following inequalities and sketch the solution set on a number line.

A.  3x - 5 > 2

Solution

        3x - 5 > 2        add 5 to both sides

        3x  > 7            divide both sides by 3

        x > 7/3

The graph is shown below.

B.  5 - 2x > 9

Solution

         5 - 2x > 1     subtract 5 from both sides.

        -2x  >  -4    divide by -2, changing the inequality sign for the negative.

         x  <  2  

The graph is shown below.

C.  -4 < 6 - 2x < 10

Solution

        -10 < 6 - 2x < 10

        -16 < -2x  <  4    Subtract 6 from all three sides.

        8  >  x  >  -2  Divide all three by -2, changing the inequality sign for the negative.

The graph is shown below.

Problem 9  

A.  Determine whether the ordered pairs (2,1) and (-1,4) are solutions to the equation

        y  =   3x +7

Solution

For the point (2,1), we plug in 2 for x and 1 for y to get

        1 = 3(2) + 7

This is false, so the point (2,1) is not a solution to the equation.

For the point (-1,4), we plug in -1 for x and 4 for y to get

        4 = 3(-1) + 7

This is a true statement, so the point (-1,4) is a solution to the equation.

B.  State which quadrant, if any, each of the following ordered pairs are in.  If the point is not in a quadrant, write "None."

(3,-5)  Quadrant ______  IV,

(4,0)  Quadrant ______  None (it is on the x-axis),

(-2,-1)  Quadrant ______  III

Problem 10 Simplify the following expression

     -7 + 3x - (4 - 8x)

Solution

First multiply the "-" sign through the parentheses by changing the sign of each term inside the parentheses.

        -7 + 3x - 4 + 8x

Now combine like terms.  Note that

        -7 - 4  =  -11    and    3x + 8x  =  11x

This gives

        -11 + 11x

e-mail Questions and Suggestions