Slope
Lines and Slope
Definition Let
(x1,y1)
and
(x2,y2) be two points then the
slope for those two
points is
rise/run
or |
Example:
For the points (1,2) and (5,-3) we have
-3 -
2
5
m =
=
5 -
1
4
|
Definition A line through a point P with slope m is the collection of points Q such that the slope between P and Q is m. |
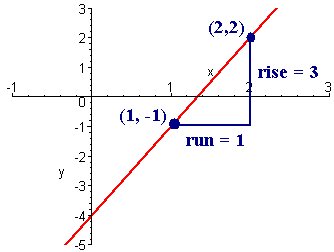
Example:
Sketch the line through the point (1,-1) with slope
m = 3.
Solution
We plot the point (1,-1)
and rise 3 and run 1 from
(1,-1) arriving at
(1 + 1,-1 + 3) = (2,2)
Then we connect
the dots.
Exercise:
Sketch the line through the point (2,-3) with slope
1/2.
Special Cases
Vertical lines have an undefined slope and horizontal lines have a zero slope.
Example:
Without graphing, describe the line through
-
(3,5) and (3,2)
-
(1,2) and (-3,2)
Solution:
-
We compute the slope:
2 - 5 3
m =
3 - 3 0
which is undefined, hence the line is vertical.
-
We compute the slope:
2 - 2 0
m =
-3 - 2 -5
hence the line is horizontal.
Exercise
Determine whether the points (1,1), (2,4), and
(7,9)
are colinear.

Back to the Math Department Home
e-mail Questions and Suggestions