Relations, Functions, and Function Notation
Definition of a Relation, Domain, and Range
Examples
-
Consider the relation that sends a student to that student's age.
-
Consider the relation that sends a student to the courses that student is taking.
-
Consider the relation that sends a parent to the parent's child.
-
Consider the relation that sends a key word either to its matches from the Yahoo search engine or to the statement "No matches found."
Each of these are examples of relations. The
definition below formalizes this idea.
|
Definition: A relation is a correspondence between two sets (called the domain and the range) such that to each element of the domain, there is assigned one or more elements of the range. |
Remark: To define a relation three things
must be designated: the range set, the domain set and the rule of
assignment.
Non-Example
Let the domain be the set of all LTCC students
and the range be the set of all math course offerings at LTCC. Then
the map that takes a student and sends the student to the math course he
or she is taking is not a relation since there are students who are not taking
math courses.
Example
(2,3), (2,4), (3,7), and (5,2)
defines a relation with
Domain: {2,3,5}
Range: {2,3,4,7}
Example
A circle represents the graph of a relation with domain consisting of x-values
from the left side of the circle to the right side. The range consists of y-values
from the bottom to the top.
Functions
A function is a special type of relation where every input has a unique output.
|
Definition: A function is a correspondence between two sets (called the domain and the range) such that to each element of the domain, there is assigned exactly one element of the range.
|
Example
(3,3), (4,3), (2,1), (6,5)
is a function with
Domain: {2,3,4,6}
Range: {1,3,5}
Non-Example:
(2,1), (5,6), (2,3), (6,7)
is not a function since 2 gets sent to more than
one value.
The Vertical Line Test
To determine whether a graph is the graph of a function, we use the
following criterion.
|
If any vertical line passes through a graph at more than one point, then the graph is not the graph of a function. Otherwise it is the graph of a function.* |
* For a more precise definition click
here
Example:
A circle is not the graph of a function as shown below.
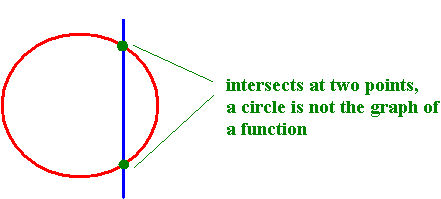
Example:
A (non-vertical) line is the graph of a function.
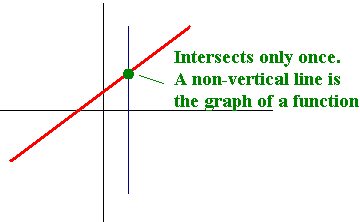
Function Notation
|
Definition We write f (x) to mean the function whose input is x. |
Example:
If
f(x) = 2x - 3
then
f(4) = 2(4) - 3 =
5
We can think of f as the function that takes the input multiplies it by
2 and subtracts 3. Sometimes it is convenient to write
f(x) without
the x. Thus:
f( ) = 2( ) - 3
whatever is in the parentheses, we put inside. For example:
f(x - 1) = 2(x - 1) - 3
and
f(x + 4) - f(x)
[2(x + 4) - 3] - [2(x) - 3]
=
4
4
2x + 8 - 3
- 2x + 3
=
Distributing
the 2 and the -
4
8
=
= 2
Combining Like Terms
4
Example
If
f(x) = 7
then
f(12) = 7
Here f is called the constant function.
Whatever comes in to f, the number 7 comes out.
Function Arithmetic
We define the sum, difference, product and quotient of functions in the obvious
way.
Example
If
x + 1
f(x) =
x - 1
and
g(x) = x2 + 4
then
x + 1
(f + g)(x) = + (x2 + 4)
x - 1
x + 1
(f - g)(x) = - (x2 + 4)
x - 1
x + 1
(f g)(x) =
(x2 + 4)
x - 1
and
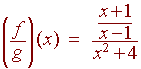
e-mail Questions and Suggestions