Sets
Set Definitions
The idea of a set is on of the fundamental concepts of
mathematics. Below, we stat the difinition.
Definition
A set is a well defined collection of objects.
Notation:
A =
{2,7,1} B = {cat, dog,
mouse} C =
{2,4,6,8,10,...100}
D = {1,3,5,7,9,...} E = {}
The set E is called the empty set.
We say that
![]()
to
mean that "6 is an element of C"
and
![]()
means "Horse is not an element of B."
Types of Numbers
-
We define the natural numbers to be
N = {1, 2, 3, 4, 5, 6, ...}
-
We define the whole numbers to be
W = {0, 1, 2, 3, 4, 5, ...}
-
We define the set of integers as
Z = {... -2, -1, 0, 1, 2, 3, ...}
So that the integers consist of the whole numbers and their negatives.
-
We define the set of rational numbers as the collection of all fractions. Formally we have
Q = { p/q | p in Z , q in Z - {0}}
Examples of Rational Numbers
3/4, 2/5, -3/2, 7, 0
Are there other numbers? What numbered squared equals?
![]()
is not a rational number.
|
We define the set of real numbers by
R = {All numbers that can be put on the number
line so that the We define the irrational numbers as the real numbers that are not rational |
Set Notation
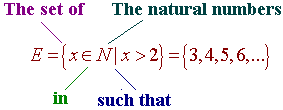
We read, "The set of all x in the natural numbers such that
x is greater
than 2"
Subsets
A is a subset of
B, A
C
B if every element of
A is also an element of
B.
Exercise
Let
A = {1,2,3), B = {0,1,2,3,4} and C = {2,3,4}
Which of the following is true? (let your mouse rest on the yellow box for a few seconds to see the solution.)
-
A C B

-
B C A

-
C C B

-
A C C

Note that we have the following chain:
|
N C W C Z C Q C R |
Unions
We define A U B "A
union
B" to be the set of all elements either in
A or B.
Example
Let
A = {1, 2,
3} B = {2, 3, 4}
then
A U B
= {1, 2, 3, 4}
Intersections
We define A I B,
"A
intersection
B" to be the set of all elements that are
in both A and
B.
A I B
= {2, 3}
from the previous example. We can write
A U B
= {x | x in A or x in B}
A I B
= {x | x in A and x in B}
Next we will discuss Venn Diagrams
To further explore with set definitions go to http://mathcsjava.emporia.edu/~godbocat/setOperations.html
e-mail Questions and Suggestions