Trigonometric Derivatives

I .   Presentations

II.  Derivative of f(x) = sin(x)

Theorem:  If f(x) = sin(x) then f'(x) = cos(x)

Proof:  We compute

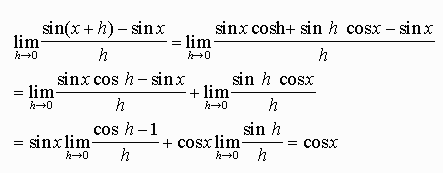
III.  d/dx cos(x)

Theorem:  If f(x) = cos(x) then f'(x) = sin(x)

Proof:  f(x) = cos(x) = sin(pi/2 - x)

Hence f'(x) = -cos(pi/2 - x) = -sin(x)

IV.  The other trig functions

Example: d/dx tan(x) = d/dx (sin(x)/cos(x)) = [cos(x)cos(x) - sin(x)(-sin(x))/(cos(x))²]

= 1/ (cos(x))² = sec² (x)

Exercise:  Show that

A.  d/dx cot(x) = -csc² (x)

B.  d/dx sec(x) = sec(x) tan(x)

C.  d/dx csc(x) = -csc(x)cot(x)

D.  d/dx ln(sec(x) + tan(x)) = sec(x)

E.  d/dx ln(sec(x) ) = tan(x)

Exercises

A.  Find the equation of the tangent line to y = 2sin(x) + cos(x) at x = pi/6

B.  Determine the relative extrema of f(x) = e^xcos(x)