Partial Derivatives

I.  Homework

II.  Definition of a Partial Derivative

Let f(x,y) be a function of two variables.  Then we define the partial derivatives as

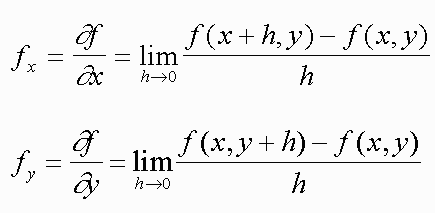
if these limits exist.  

Algebraically, we can think of the partial derivative of a function with respect to x as the derivative of the function with y held constant.  Geometrically, the derivative with respect to x at a point P represents the slope of the curve that passes through P whose projection onto the xy plane is a horizontal line.  (If you travel due East, how steep are you climbing?)

Example

Let f(x,y) = 2x + 3y then

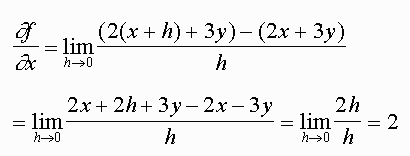
Exercise:  Find delf/dely for the function above.

III.  Finding Partial Derivatives the Easy Way

Since a partial derivative with respect to x is a derivative with the rest of the variables held constant, we can find the partial derivative by taking the regular derivative considering the rest of the variables as constants.

Example:  Let f(x,y)  = 3xy² - 2x²y

then f_x = 3y² - 4xy

Exercise:  Find f_y

More Exercises

 Find both partial derivatives for

A)  f(x,y) = xye^x 

B)  f(x,y) = (x + y)/(x - y)

IV.  Higher Order Partials

Just as with regular derivatives, we can define second derivatives.  For functions of two variables, we have four types:

f_xx, f_xy, f_yx, and f_yy. We will also see the del notation in class.

Example

Let f(x,y) = ye^x  

then delf/delx = ye^x, delf/dely = e^x

Now taking the partials of each of these we get:

f_xx = ye^x , f_xy = e^x, f_yx = e^x, and f_yy = 0

Notice that    f_xy =  f_yx  

Theorem:  Let f(x,y) be a function with continuous second order derivatives, then    f_xy =  f_yx  

V)  Functions of More Than Two Variables

Suppose that f(x,y,z)  = xy - 2yz is a function of three variables, then we can define the partial derivatives in much the same way as we defined the partial derivatives for three variables.  

We have

f_x = y , f_y = x - 2z and f_z = -2y