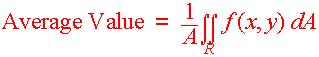Double Integrals and Volume
Definition of Volume
Recall that area between two curves is defined as the integral of the top curve minus the bottom curve. This idea can be brought to three dimensions. We defined the volume between two surfaces as the double integral of the top surface minus the bottom surface. This can be written formally with the theorem below.
|
Fubini's Theorem Let f, g1, g2, h1, and h2 be defined and continuous on a region R. Then the volume of the surface is equal to the double integrals: |
Notice that all the typical properties of the double integral hold. For example, constants can be pulled out and the double integral of the sum of two functions is the sum of the double integrals of each function.
Finding Volume
Example
Set up the integral to find the volume of the solid that lies below the cone
![]()
and above the xy-plane.
Solution
The cone is sketched below
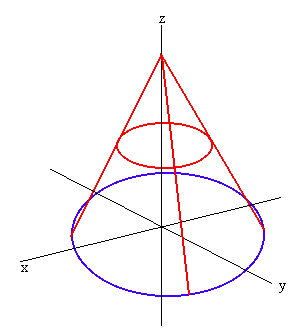
We can see that the region R is the blue circle in the xy-plane. We can find the equation by setting z = 0.
![]()
Solving for y (by moving the square root to the left hand side, squaring both sides, etc) gives
![]()
The "-" gives the lower limit and the "+" gives the upper limit. For the outer limits, we can see that
-4 < x < 4
Putting this all together gives
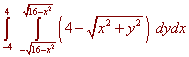
Either by hand or by machine we can obtain the result
Volume = 64 p/3
Notice that this agrees with the formula
Volume = p r2h/3
Exercise
Set up the double integral for this problem with dxdy instead of dydx. Then show that the two integrals give the same result.
Example
Set up the double integral that gives the volume of the solid that lies below the sphere
x2 + y2 + z2 = 6
and above the paraboloid
z = x2 + y2
Solution

The picture below indicated that the region is the disk that lies inside that circle of intersection of the two surfaces. We substitute
x2 + y2 + (x2 + y2)2 = 6
or
x2 + y2 + (x2 + y2)2 - 6 = 0
Now factor with x2 + y2 as the variable to get
(x2 + y2 - 2)(x2 + y2 + 3) = 0
The second factor has no solution, while the first is
x2 + y2 = 2
Solving for y gives
![]()
and
-![]() <
x <
<
x < ![]()
Just as we did in one variable calculus, the volume between two surfaces is the double integral of the top surface minus the bottom surface. We have
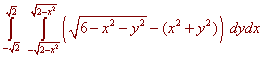
Again we can perform this integral by hand or by machine and get
Volume = 7.74
Average Value
We think of the average as the sum of all divided by the total. The double integral acts as the sum and the total is the area. This leads us to the following definition.
| Let f(x,y)
be an integrable function over the region R
with area A,
then the Average Value
of of f
over R
is
|
Example
You sell T-shirts and sweatshirts and have determined that the profit function for selling x T-shirts and y sweatshirts is given by
P(x,y) = 10000 +2100 x - 3x2 + 3(y - 400)2
Find the average profit if you sell between 200 and 400 T-shirts and between 300 and 400 sweatshirts.
Solution
We find the double integral
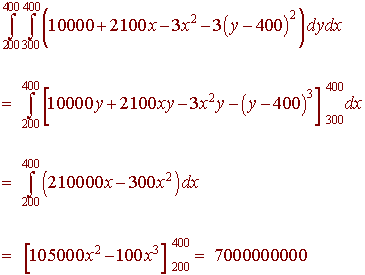
Next divide by the total area
A = (400 - 300)(400 - 200) = 20000
to get
Average Profit = 350000
or 3,500 dollars.
Population
Suppose the population density of ants at a location (x,y) in meters, where the origin corresponds to the water source can be modeled by
30000
P(x,y)
=
1+ x2 + y2
Set up the integral that estimates the total ant population within 100 meters of the water source. Then use a calculator to evaluate this integral.
Solution
The region is the circle of radius 100
x2 + y2 = 10000
We find
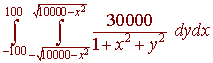
The calculator gives us a population of about 868,000 ants.
Back to the Math 117 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions