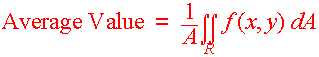Double Integrals and Volume

Definition of Volume

Recall that area between two curves is defined as the integral of the top curve minus the bottom curve.  This idea can be brought to three dimensions.  We defined the volume between two surfaces as the double integral of the top surface minus the bottom surface.  This can be written formally with the theorem below.

Notice that all the typical properties of the double integral hold.  For example, constants can be pulled out and the double integral of the sum of two functions is the sum of the double integrals of each function.

Finding Volume

Example

Set up the integral to find the volume of the solid that lies below the cone

and above the xy-plane.  

Solution

The cone is sketched below

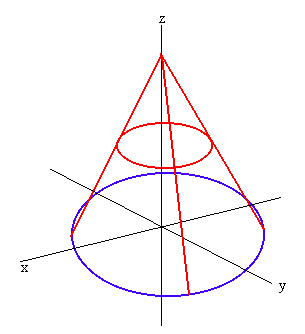
We can see that the region R is the blue circle in the xy-plane.  We can find the equation by setting z  =  0.

Solving for y (by moving the square root to the left hand side,  squaring both sides, etc) gives

The "-" gives the lower limit and the "+" gives the upper limit.  For the outer limits, we can see that 

        -4  <  x  <  4

Putting this all together gives

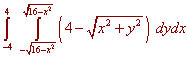
Either by hand or by machine we can obtain the result 

        Volume  =  64 p/3

Notice that this agrees with the formula 

        Volume  =  p r²h/3

Exercise

Set up the double integral for this problem with dxdy instead of dydx.  Then show that the two integrals give the same result.

Example

Set up the double integral that gives the volume of the solid that lies below the sphere

        x² + y² + z²  =  6

and above the paraboloid 

        z  =  x² + y² 

Solution

The picture below indicated that the region is the disk that lies inside that circle of intersection of the two surfaces.  We substitute

        x² + y² + (x² + y²)²  =  6

or

        x² + y² + (x² + y²)² - 6  =  0

Now factor with x² + y² as the variable to get

        (x² + y² - 2)(x² + y² + 3)  =  0

The second factor has no solution, while the first is 

        x² + y²  =  2

Solving for y gives

and

        -  <  x  < 

Just as we did in one variable calculus, the volume between two surfaces is the double integral of the top surface minus the bottom surface.  We have

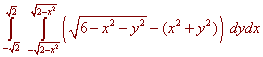
Again we can perform this integral by hand or by machine and get

        Volume  =  7.74

Average Value

We think of the average as the sum of all divided by the total.  The double integral acts as the sum and the total is the area.  This leads us to the following definition.

Example

You sell T-shirts and sweatshirts and have determined that the profit function for selling x T-shirts and y sweatshirts is given by 

        P(x,y)  =  10000 +2100 x - 3x² + 3(y - 400)² 

Find the average profit if you sell between 200 and 400 T-shirts and between 300 and 400 sweatshirts.

Solution

We find the double integral

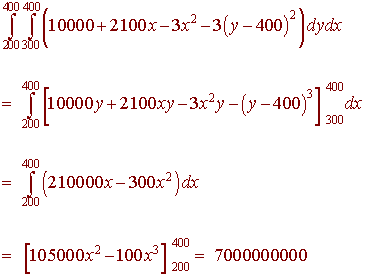
Next divide by the total area

        A  =  (400 - 300)(400 - 200)  =  20000

to get

        Average Profit  =  350000

or 3,500 dollars.

Population

Suppose the population density of ants at a location (x,y) in meters, where the origin corresponds to the water source can be modeled by 

                               30000
         P(x,y)  =                          
                            1+ x² + y²

Set up the integral that estimates the total ant population within 100 meters of the water source.  Then use a calculator to evaluate this integral.

Solution

The region is the circle of radius 100

        x² + y²  =  10000

We find 

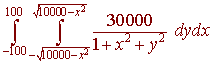
The calculator gives us a population of about 868,000 ants.

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions