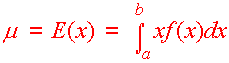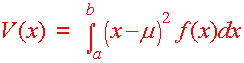Expected Value and Variance

Expected Value

We have seen that for a discrete random variable, that the expected value is the sum of all xP(x).  For continuous random variables, P(x) is the probability density function, and integration takes the place of addition.  

Remark:  Integration by parts and/or substitution will typically be used to perform the integration.

Example

Find the expected value of the density function defined by

        f(x)  =  sin(x)        0  <  x  <  p/2

Solution

We compute the integral

We use integration by parts with

        u  =  x        dv  =  sin(x) dx
      du  =  dx     v  =  -cos(x)

We have

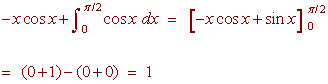
Variance and Standard Deviation

The variance formula for a continuous random variable also follows from the variance formula for a discrete random variable.  Once again we interpret the sum as an integral. 

Example

Use a calculator to find the variance and standard deviation of the density function

        f(x)  =  6x - 6x²         0  <  x  <  1

Solution

We first need to find the expected value.  We have

Now we can compute the variance

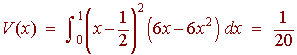
Finally the standard deviation is the square root of the variance or

        s  =  0.22

The Median

The expected value is what you are used to as the average.  Another useful number is the median which gives the halfway point.  Since the total area under a probability density function is always equal to one, the halfway point of the data will be the x-value such that the area from the left to the median under f(x) is equal to 1/2.  

Example

Find the median of the probability density function

                       1
        f(x)  =            x²         3 < x < 6
                      63

Solution

We integrate

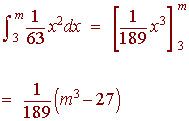
Now we set the above equal to 1/2 and solve.

        m³ - 27  =  94.5

       m³  =  121.5

       m  =  4.95

The Uniform Density Function

If every interval of a fixed length is equally likely to occur then we call the probability density function the uniform density function.  It has formula

                          1
        f(x)  =                            a < x < b  
                       b - a

Example

The distribution of insects along a fallen log of length twenty feet is uniform.  Find the standard deviation for this distribution.

Solution

First notice that the density function is given by 

                          1
        f(x)  =                      0  <  x  <  20     
                       20

The expected value is given by 

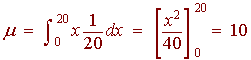
Next, we find the variance.  We have

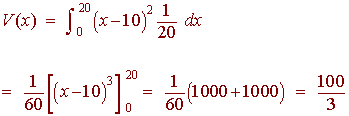
The standard deviation is the square root 

        s  =  5.77

The Normal Distribution 

The most important distribution for working with statistics is called the normal distribution.  If with mean m and standard deviation s the density function is given by

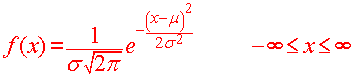
Exercise

Show that the expected value of the normal distribution is m.

The Exponential Distribution

Another important distribution is call the exponential distribution.  It has density function

Exercise

Find the mean and standard deviation of the exponential distribution.

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions