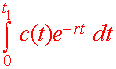Integration by Parts
Derivation of Integration by Parts
Recall the product rule:
(uv)' = u' v + uv'
or
uv' = (uv)' - u' v
Integrating both sides, we have that
![]() uv' dx
=
uv' dx
= ![]() (uv)'
dx -
(uv)'
dx - ![]() u'
v dx
u'
v dx
= uv - ![]() u'
v
dx.
u'
v
dx.
|
Theorem: Integration by Parts Let u and v be differentiable functions, then
|
Examples
Integrate
![]()
Solution
We use integration by parts. Notice that we need to use substitution to find the integral of ex.
| u = x | dv= e3x dx |
| du = dx | v = 1/3 e3x |
Hence we have
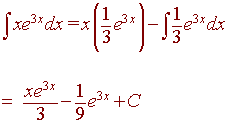
Exercise
Evaluate
![]() x ln x dx
x ln x dx ![]()
Integration By Parts Twice
Example
Evaluate
![]() x2 ex dx
x2 ex dx
We use integration by parts
| u = x2 | dv = ex dx |
| du = 2x dx | v = ex |
We have
x2ex - ![]() 2xex dx
= x2ex - 2
2xex dx
= x2ex - 2![]() xex dx
xex dx
Have we gone nowhere? Now we now use integration by parts a second time to find this integral
| u = x | dv = ex dx |
| du = dx | v = ex |
We get
x2ex
- 2xex + 2![]() ex dx
ex dx
= x2ex - 2xex + 2ex + C
Other By Parts
Occasionally there is not an obvious pair of u and dv. This is where we get creative.
Example:
Find
![]() ln x dx
ln x dx
What should we let u and dv be? Try
| u = ln x | dv = dx |
| du = 1/x dx | v = x |
We get
x lnx
- ![]() dx
= x lnx - x + C
dx
= x lnx - x + C
When to Use Integration By Parts
- When
u-substitution does not work
- When there is a mix of two types of functions such as an exponential
and polynomial, polynomial and log, etc.
- With ln
x.
- When all else fails.
Evaluating a Definite Integral
We can use integration by parts to evaluate definite integrals. We just have to remember that all terms receive the limits.
Example
Evaluate
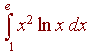
Solution
Use integration by parts
| u = ln x | dv = x2 dx |
| du = 1/x dx | v = 1/3 x3 |
We get
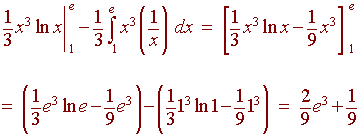
Application: Present Value
Your patent brings you a annual income of 3,000 t dollars where t is the number of years since the the patent begins. The patent will expire in 20 years. A business has offered to purchase the patent from you. How much should you ask for it? Assume an inflation rate of 5%.
This question is a present value problem. Since there is inflation, your later earnings will be worth less than this year's earnings. The formula to determine this is given by
|
Present Value Formula If c(t) is the continuous annual income over t1 years with an inflation rate r, then the present value can by found by
|
For our example, we have
c(t) = 2000 t r = 0.05 t1 = 20
We integrate
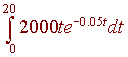
Use integration by parts and note that with the substitution
u = -0.05t du = -0.05dt
or
-20du = dt
we get
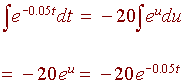
so that
| u = 2000t | dv = e-0.05t dt |
| du = 2000 dt | v = -20e-0.05t |
This gives us
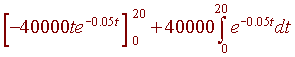
We have already found the antiderivative for this last integral. We have
![]()
You should ask for $211,393.
Back to the Math 116 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions