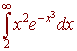Math 116 Practice Final Key
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work
Problem 1 Find the derivative of the following functions
Solution
We use the chain rule. We have
u = 1 - x u' = -1
v = ln(u) v' = 1/u
f(v) = ln(v) f '(v) = 1/v
Hence
f '(x) = (-1)(1/u)(1/v)
-1
=
(1 - x)(ln(1 - x))
Solution
We have
![]()
Let
u = x2ln x u' = 2x ln x + x2(1/x) = 2x ln x + x
f(u) = eu f '(u) = eu
Hence
f '(x) = eu (2x ln x + x)
![]()
Solution
We use the quotient rule. We have
(sin x)ex - ex(cos
x)
ex(sin x - cos x)
f '(x)
=
=
sin2
x
sin2 x
Problem 2 Evaluate the following integrals
Solution
We use integration by parts
u = x dv = e2x dx w = 2x dw = 2dx 1/2 dw = dx
du = dx v = 1/2 e2x
We get

We use partial fractions here
3x +
1
A
B
=
+
x2 - x -
6 x -
3 x + 2
or
3x + 1 = A(x + 2) + B(x - 3)
Let x = 3: 10 = 5A A = 2
Let x = -2: -5 = -5B B = 1
This gives us
![]()
We use u-substitution
u = 2x + 1 du = 2dx
x = 1/2 u - 1/2 dx = 1/2 du
We have

Solution
This is an improper integral, we use u-substitution with
u = x3 du = 3x2 dx 1/3u = x2 dx
We have

Solution
We let
u = cos x du = -sin x dx
We get

Find the volume of the solid formed by revolving the region bounded by the curves
y = x2 + 4 and y = 5x
about the x-axis.
Solution
We first graph the two equations and revolve a cross section about the x-axis.

To find the intersection points, we set the equations equal to each other. We have
x2 + 4 = 5x
x2 - 5x + 4 = 0
(x - 4)(x - 1) = 0
x = 4 or x = 1
Notice that the top curve is y = 5x and the bottom curve is y = x2 + 4. The area of the washer is
A = pR2 - pr2
R = 5x r = x2 + 4
Putting this all together gives

In 1980 there were 200 reported cases of the HIV virus. Is has been predicted that the number of HIV cases will eventually level off at about 80,000,000. Determine the year when the number infected will hit 50,000,000 solving the differential equation
dP
= .01P(80,000,000 - P)
dt
Solution
We integrate
![]()
The right hand integral is 0.3t + C. For the left hand integral we use partial fractions. We have
1
A
B
=
+
P(80,000,000 -
P)
P
80,000,000 - P
So that
1 = A(80,000,000 - P) + BP
Let P = 80,000,000: 1 = 80,000,000B B = 1/80,000,000
Let P = 0: 1 = 80,000,000A A = 1/80,000,000
Now integrate to get
1
1
lnP -
ln(80,000,000 - P) = .01t + C
80,000,000
80,000,000
Multiplying by 80,000,000 gives
lnP - ln(80,000,000 - P) = 24,000,000t + M M = 80,000,000C
Plugging in P = 200 when t = 0 gives
M = ln 200 - ln(80,000,000 - 200) = -12.9
We want the year when P = 50,000,000. We have
ln 50,000,000 - ln 30,000,000 = 0.3t - 12.9
.51 = 0.3t - 12.9 t = 44.7
We can conclude that in 2025, the HIV virus will have infected 50,000,000 people.
The GNP growth since 1980 can be modeled by the equation
y = 3 cos(0.8t) + 2
A. Find the period of this function and explain what this says about growth.
Solution
We have
Period = 2p/.8 = 7.85
This means that there is a growth cycle that repeats itself every 7.85 years.
B. What is the maximum growth and when does it occur? (Use calculus to show this).
Solution
We find the derivative using the chain rule.
u = .8t u' = .8
f(u) = 3cos u + 2 f '(u) = -3sin u
y' = (.8)(-3sin(.8t)) = -2.4sin(.8t)
This is zero when
.8t = kp t = kp/.8 = 3.9k
The second derivative is
y'' = (.8)(-cos(.8t))
which is negative for k even. Hence the maximum occurs every 7.85 years beginning towards the end of 1980. The maximum is
3 cos(0.8(0)) + 2 = 5
The rate of which a pill is dissolved when it enters the body is given by
dy
et
=
dt
1 + t2
Use Simpson's Rule with n = 4 to determine the total amount of the pill that is dissolved during the first 4 minutes.
Solution
We have
(4 -
0) e0
e1
e2
e3
e4
[
+
+
+
+
]
3(4) 1 + 02
1 + 12 1 + 22
1 + 32 1 + 42
= 3.02
Find the area between the curves
y = ln x y = sin x x = 1 and x = 2
Solution
We sketch the graph
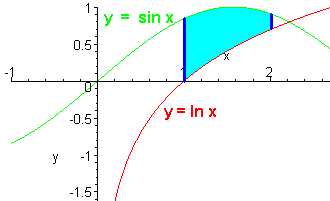
We see that the top curve is y = sin x and the bottom curve is y = ln x. We have

The second integral is the challenge. We use integration by parts.
u = ln x dv = dx
du = 1/x dx v = x
We have