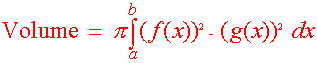Discs and Washers
Volumes of Revolution
Suppose you wanted to make a clay vase. It is made by
shaping the clay into a curve and spinning it along an axis. If we want to
determine how much water it will hold, we can consider the cross sections that
are perpendicular to the axis of rotation, and add up all the volumes of the
small cross sections. We have the following definition:
|
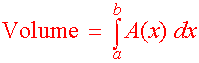
where A(x) is the area the cross section at a point
x.
Disks
Example
Find the volume of the solid that is produced when the region
bounded by the curve
y = x2
y = 0 and
x = 2
is revolved around the x-axis.
Solution
Since we are revolving around the x-axis, we have that the cross section is in the shape of a disk with radius equal to the y-coordinate of the point.
Hence
A(x) = pr2
= p[x2]2
We have
| Volume by Disks
If the region below y = f(x), above the x-axis, and between the lines x = a and x = b is revolved around the x-axis, then the volume of the resulting solid is given by
|
Example: Washers
Find the volume of the solid formed be revolving the region
between the curves
y = x2 and
y = 
about the x-axis.
Solution
We draw the picture and revolve a cross section about the x-axis and come up with a washer.
The area of the Washer is equal to the area of the outer disk
minus the area of the inner disk.
|
A = p(R2 - r2) |
We have that R is the y-coordinate of the top curve
(y = )
and r is the y-coordinate of the bottom curve (y
= x2).
We have
A
= p(2
- [x2]2) = p[x - x4]
Hence
In general, we have
| Volume by Washers
If the region below y = f(x), above the y = g(x), and between the lines x = a and x = b is revolved around the x-axis, then the volume of the resulting solid is given by
|
Back to the Math 116 Home Page